Advertisements
Advertisements
प्रश्न
Jayanti takes shortest route to her home by walking diagonally across a rectangular park. The park measures 60 metres × 80 metres. How much shorter is the route across the park than the route around its edges?
Advertisements
उत्तर
As the park is rectangular, all the angles area of 90°
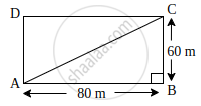
In right angled ΔABC,
AC2 = AB2 + BC2 ...[By Pythagoras theorem]
⇒ AC2 = (60)2 + (80)2 = 3600 + 6400
⇒ AC2 = 10000
⇒ AC = `sqrt(10000)`
⇒ AC = 100 m
If she goes through AB and AC, then the total distance covered = (60 + 80) m = 140 m
∴ Difference between two paths = (140 – 100) m = 40 m.
APPEARS IN
संबंधित प्रश्न
The diagonal of a rectangular field is 16 metres more than the shorter side. If the longer side is 14 metres more than the shorter side, then find the lengths of the sides of the field.
In figure, ∠B of ∆ABC is an acute angle and AD ⊥ BC, prove that AC2 = AB2 + BC2 – 2BC × BD
ABC is a right triangle right-angled at C. Let BC = a, CA = b, AB = c and let p be the length of perpendicular from C on AB, prove that
(i) cp = ab
`(ii) 1/p^2=1/a^2+1/b^2`
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals
In the given figure, ABC is a triangle in which ∠ABC> 90° and AD ⊥ CB produced. Prove that AC2 = AB2 + BC2 + 2BC.BD.
In the given figure, angle ADB = 90°, AC = AB = 26 cm and BD = DC. If the length of AD = 24 cm; find the length of BC.
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = AE2 + CD2 + BF2
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that: 9BP2 = 9BC2 + 4AC2
∆ABC is right-angled at C. If AC = 5 cm and BC = 12 cm. find the length of AB.
Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
