Advertisements
Advertisements
प्रश्न
The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is
(A)\[7 + \sqrt{5}\]
(B) 5
(C) 10
(D) 12
उत्तर
Let us plot these coordinates, i.e. O(0, 0), A(0, 4) and B(3, 0), on the Cartesian plane.
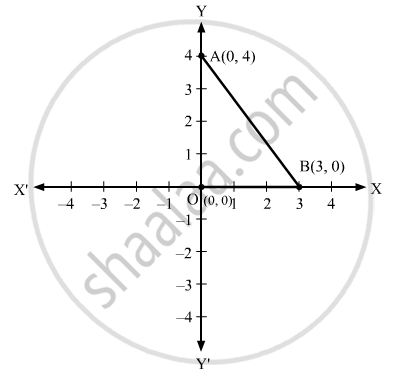
We can observe that triangle AOB is a right-angled triangle with OB = 3 units and OA = 4 units.
Now, AB2 = OA2 + OB2 (By Pythagoras theorem)
⇒ AB2 = (42 + 32) sq. units
= (16 + 9) sq. units
= 25 sq. units
⇒ AB = 5 units
Perimeter of ∆AOB = OA + AB + BO
= (3 + 5 + 4) units
= 12 units
Hence, the correct option is D.
APPEARS IN
संबंधित प्रश्न
The diagonal of a rectangular field is 16 metres more than the shorter side. If the longer side is 14 metres more than the shorter side, then find the lengths of the sides of the field.
In ΔABC, Find the sides of the triangle, if:
- AB = ( x - 3 ) cm, BC = ( x + 4 ) cm and AC = ( x + 6 ) cm
- AB = x cm, BC = ( 4x + 4 ) cm and AC = ( 4x + 5) cm
ABC is a triangle, right-angled at B. M is a point on BC.
Prove that: AM2 + BC2 = AC2 + BM2
In Fig. 3, ∠ACB = 90° and CD ⊥ AB, prove that CD2 = BD x AD.

In the given figure, angle ADB = 90°, AC = AB = 26 cm and BD = DC. If the length of AD = 24 cm; find the length of BC.

Two poles of height 9m and 14m stand on a plane ground. If the distance between their 12m, find the distance between their tops.
In a right-angled triangle ABC,ABC = 90°, AC = 10 cm, BC = 6 cm and BC produced to D such CD = 9 cm. Find the length of AD.
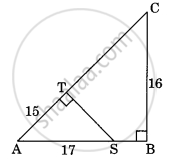
In the given figure, ∠T and ∠B are right angles. If the length of AT, BC and AS (in centimeters) are 15, 16, and 17 respectively, then the length of TC (in centimeters) is ______.
If ΔABC ~ ΔPQR, `("ar" triangle "ABC")/("ar" triangle "PQR") = 9/4` and AB = 18 cm, then the length of PQ is ______.
If S is a point on side PQ of a ΔPQR such that PS = QS = RS, then ______.
