Advertisements
Advertisements
प्रश्न
In ΔABC, Find the sides of the triangle, if:
- AB = ( x - 3 ) cm, BC = ( x + 4 ) cm and AC = ( x + 6 ) cm
- AB = x cm, BC = ( 4x + 4 ) cm and AC = ( 4x + 5) cm
उत्तर
(i) In right-angled ΔABC,
AC2 = AB2 + BC2
⇒ ( x + 6 )2 = ( x - 3 )2 + ( x + 4 )2
⇒ ( x2 + 12x + 36 ) = ( x2 - 6x + 9 ) + ( x2 + 8x + 16 )
⇒ x2 - 10x - 11 = 0
⇒ ( x - 11 )( x + 1 ) = 0
⇒ x = 11 or x = - 1
But length of the side of a triangle can not be negative.
⇒ x = 11 cm
∴ AB = ( x - 3 ) = ( 11 - 3 ) = 8 cm
BC = ( x + 4 ) = ( 11 + 4 ) = 15 cm
AC = ( x + 6 ) = ( 11 + 6 ) = 17 cm.
(ii) In right-angled ΔABC,
AC2 = AB2 + BC2
⇒ ( 4x + 5 )2 = ( x )2 + ( 4x + 4 )2
⇒ ( 16x2 + 40x + 25 ) = ( x2 ) + ( 16x2 + 32x + 16 )
⇒ x2 - 8x - 9 = 0
⇒ ( x - 9 )( x + 1 ) = 0
⇒ x = 9 or x = - 1
But length of the side of a triangle can not be negative.
⇒ x = 9 cm
∴ AB = x = 9 cm
BC = ( 4x + 4 ) = ( 36 + 4 ) = 40 cm
AC = ( 4x + 5 ) = ( 36 + 5 ) = 41 cm.
APPEARS IN
संबंधित प्रश्न
Sides of triangles are given below. Determine it is a right triangles? In case of a right triangle, write the length of its hypotenuse. 3 cm, 8 cm, 6 cm
In the given figure, ABC is a triangle in which ∠ABC < 90° and AD ⊥ BC. Prove that AC2 = AB2 + BC2 − 2BC.BD.

Prove that, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the square of remaining two sides
Digonals of parallelogram WXYZ intersect at point O. If OY =5, find WY.

In ΔMNP, ∠MNP = 90˚, seg NQ ⊥ seg MP, MQ = 9, QP = 4, find NQ.
In the following figure, AD is perpendicular to BC and D divides BC in the ratio 1: 3.
Prove that : 2AC2 = 2AB2 + BC2
In triangle ABC, AB = AC and BD is perpendicular to AC.
Prove that: BD2 - CD2 = 2CD × AD
Find the Pythagorean triplet from among the following set of numbers.
2, 4, 5
Find the length of the hypotenuse of a triangle whose other two sides are 24cm and 7cm.
In an equilateral triangle ABC, the side BC is trisected at D. Prove that 9 AD2 = 7 AB2.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AC2 - AB2 = 2BC x ED
In a square PQRS of side 5 cm, A, B, C and D are points on sides PQ, QR, RS and SP respectively such as PA = PD = RB = RC = 2 cm. Prove that ABCD is a rectangle. Also, find the area and perimeter of the rectangle.
There are two paths that one can choose to go from Sarah’s house to James's house. One way is to take C street, and the other way requires to take B street and then A street. How much shorter is the direct path along C street?

Find the length of the support cable required to support the tower with the floor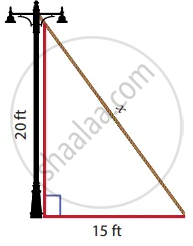
Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
Two rectangles are congruent, if they have same ______ and ______.
Two circles having same circumference are congruent.
Jiya walks 6 km due east and then 8 km due north. How far is she from her starting place?
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its top reach?
