Advertisements
Advertisements
प्रश्न
Find the length of the hypotenuse of a triangle whose other two sides are 24cm and 7cm.
उत्तर
The two sides (excluding hypotenuse) of a right-angled triangle are given as 24cm and 7cm
(hypotenuse)2 = (24cm)2 + (7cm)2
(hypotenuse)2 = 576cm2 + 49cm2
(hypotenuse)2 = 625cm2
(hypotenuse)2 = (25cm)2
Thus, the length of the hypotenuse of the triangle is 25cm.
APPEARS IN
संबंधित प्रश्न
In Fig., ∆ABC is an obtuse triangle, obtuse angled at B. If AD ⊥ CB, prove that AC2 = AB2 + BC2 + 2BC × BD
ABCD is a rhombus. Prove that AB2 + BC2 + CD2 + DA2= AC2 + BD2
P and Q are the mid-points of the sides CA and CB respectively of a ∆ABC, right angled at C. Prove that:
`(i) 4AQ^2 = 4AC^2 + BC^2`
`(ii) 4BP^2 = 4BC^2 + AC^2`
`(iii) (4AQ^2 + BP^2 ) = 5AB^2`
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AD2 = BD × CD

Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals
In the following figure, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that

(i) OA2 + OB2 + OC2 − OD2 − OE2 − OF2 = AF2 + BD2 + CE2
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2
In an equilateral triangle ABC, D is a point on side BC such that BD = `1/3BC` . Prove that 9 AD2 = 7 AB2
Prove that the points A(0, −1), B(−2, 3), C(6, 7) and D(8, 3) are the vertices of a rectangle ABCD?
For finding AB and BC with the help of information given in the figure, complete following activity.
AB = BC .......... 
∴ ∠BAC = 
∴ AB = BC =  × AC
× AC
=  × `sqrt8`
× `sqrt8`
=  × `2sqrt2`
× `2sqrt2`
= 

Find the length diagonal of a rectangle whose length is 35 cm and breadth is 12 cm.
Digonals of parallelogram WXYZ intersect at point O. If OY =5, find WY.
In the given figure, ∠B = 90°, XY || BC, AB = 12 cm, AY = 8cm and AX : XB = 1 : 2 = AY : YC.
Find the lengths of AC and BC.

AD is perpendicular to the side BC of an equilateral ΔABC. Prove that 4AD2 = 3AB2.
The perpendicular PS on the base QR of a ∆PQR intersects QR at S, such that QS = 3 SR. Prove that 2PQ2 = 2PR2 + QR2
Find the unknown side in the following triangles
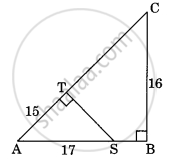
In the given figure, ∠T and ∠B are right angles. If the length of AT, BC and AS (in centimeters) are 15, 16, and 17 respectively, then the length of TC (in centimeters) is ______.
In figure, PQR is a right triangle right angled at Q and QS ⊥ PR. If PQ = 6 cm and PS = 4 cm, find QS, RS and QR.
If the areas of two circles are the same, they are congruent.
The hypotenuse (in cm) of a right angled triangle is 6 cm more than twice the length of the shortest side. If the length of third side is 6 cm less than thrice the length of shortest side, then find the dimensions of the triangle.
