Advertisements
Advertisements
प्रश्न
The hypotenuse (in cm) of a right angled triangle is 6 cm more than twice the length of the shortest side. If the length of third side is 6 cm less than thrice the length of shortest side, then find the dimensions of the triangle.
उत्तर
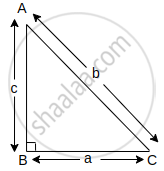
Let ΔABC be the right angle triangle, right angled at B, as shown in the figure.
Also, let AB = c cm, BC = a cm and AC = b cm
Then, according to the given information, we have
b = 6 + 2a .....(i) (Let a be the shortest side)
and c = 3a – 6 ...(ii)
We know that, b2 = c2 + a2
⇒ (6 + 2a)2 = (3a – 6)2 + a2 ...[Using (i) and (ii)]
⇒ 36 + 4a2 + 24a = 9a2 + 36 – 36a + a2
⇒ 60a = 6a2
⇒ 6a = 60 ...[∵ a cannot be zero]
⇒ a = 10 cm
Now, from equation (i),
b = 6 + 2 × 10 = 26
and from equation (ii),
c = 3 × 10 – 6 = 24
Thus, the dimensions of the triangle are 10 cm, 24 cm and 26 cm.
संबंधित प्रश्न
In a right triangle ABC, right-angled at B, BC = 12 cm and AB = 5 cm. The radius of the circle inscribed in the triangle (in cm) is
(A) 4
(B) 3
(C) 2
(D) 1
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2 + BD2 = AB2 + DE2
Find the side and perimeter of a square whose diagonal is 10 cm.
Prove that `(sin θ + cosec θ)^2 + (cos θ + sec θ)^2 = 7 + tan^2 θ + cot^2 θ`.
In the given figure, angle BAC = 90°, AC = 400 m, and AB = 300 m. Find the length of BC.

In triangle PQR, angle Q = 90°, find: PR, if PQ = 8 cm and QR = 6 cm
AD is perpendicular to the side BC of an equilateral ΔABC. Prove that 4AD2 = 3AB2.
There are two paths that one can choose to go from Sarah’s house to James's house. One way is to take C street, and the other way requires to take B street and then A street. How much shorter is the direct path along C street?

The perpendicular PS on the base QR of a ∆PQR intersects QR at S, such that QS = 3 SR. Prove that 2PQ2 = 2PR2 + QR2
