Question

The hypotenuse (in cm) of a right angled triangle is 6 cm more than twice the length of the shortest side. If the length of third side is 6 cm less than thrice the length of shortest side, then find the dimensions of the triangle.

Answer 1

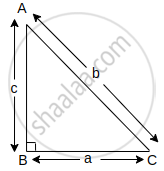
Let ΔABC be the right angle triangle, right angled at B, as shown in the figure.

Also, let AB = c cm, BC = a cm and AC = b cm

Then, according to the given information, we have

b = 6 + 2a  .....(i) (Let a be the shortest side)

and c = 3a – 6  ...(ii)

We know  that, b² = c² + a²

⇒ (6 + 2a)² = (3a – 6)² + a²  ...[Using (i) and (ii)]

⇒ 36 + 4a² + 24a = 9a² + 36 – 36a + a²

⇒ 60a = 6a²

⇒ 6a = 60  ...[∵ a cannot be zero]

⇒ a = 10 cm

Now, from equation (i),

b = 6 + 2 × 10 = 26

and from equation (ii),

c = 3 × 10 – 6 = 24

Thus, the dimensions of the triangle are 10 cm, 24 cm and 26 cm.