Advertisements
Advertisements
प्रश्न
AD is drawn perpendicular to base BC of an equilateral triangle ABC. Given BC = 10 cm, find the length of AD, correct to 1 place of decimal.
उत्तर
Since ABC is an equilateral triangle therefore, all the sides of the triangle are of the same measure and the perpendicular AD will divide BC into two equal parts.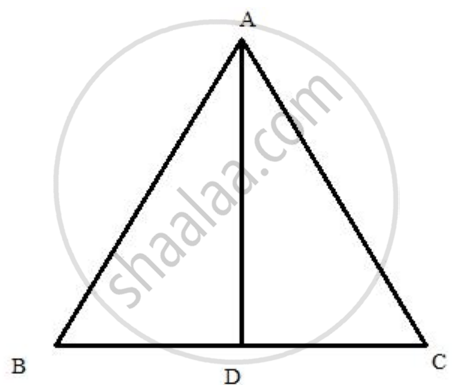
Pythagoras theorem states that in a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
Here, we consider the ΔABD and applying Pythagoras theorem we get,
AB2 = AD2 + BD2
AD2 = 102 - 52 ......[ Given, BC = 10 cm = AB, BD = `1/2` BC ]
AD2 = 100 - 25
AD2 = 75
AD = 8.7
Therefore, the length of AD is 8.7 cm
APPEARS IN
संबंधित प्रश्न
Prove that the diagonals of a rectangle ABCD, with vertices A(2, -1), B(5, -1), C(5, 6) and D(2, 6), are equal and bisect each other.
In Figure ABD is a triangle right angled at A and AC ⊥ BD. Show that AC2 = BC × DC

In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AD2 = BD × CD

In ∆ABC, AB = 10, AC = 7, BC = 9, then find the length of the median drawn from point C to side AB.
A man goes 40 m due north and then 50 m due west. Find his distance from the starting point.
In the given figure, AB//CD, AB = 7 cm, BD = 25 cm and CD = 17 cm;
find the length of side BC.
In figure AB = BC and AD is perpendicular to CD.
Prove that: AC2 = 2BC. DC.
O is any point inside a rectangle ABCD.
Prove that: OB2 + OD2 = OC2 + OA2.
Prove that `(sin θ + cosec θ)^2 + (cos θ + sec θ)^2 = 7 + tan^2 θ + cot^2 θ`.
In ∆ ABC, AD ⊥ BC.
Prove that AC2 = AB2 +BC2 − 2BC x BD
A boy first goes 5 m due north and then 12 m due east. Find the distance between the initial and the final position of the boy.
Use the information given in the figure to find the length AD.

Find the length of the hypotenuse of a triangle whose other two sides are 24cm and 7cm.
In an equilateral triangle ABC, the side BC is trisected at D. Prove that 9 AD2 = 7 AB2.
AD is perpendicular to the side BC of an equilateral ΔABC. Prove that 4AD2 = 3AB2.
In a right-angled triangle ABC,ABC = 90°, AC = 10 cm, BC = 6 cm and BC produced to D such CD = 9 cm. Find the length of AD.
Determine whether the triangle whose lengths of sides are 3 cm, 4 cm, 5 cm is a right-angled triangle.
There are two paths that one can choose to go from Sarah’s house to James's house. One way is to take C street, and the other way requires to take B street and then A street. How much shorter is the direct path along C street?

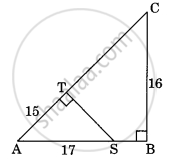
In the given figure, ∠T and ∠B are right angles. If the length of AT, BC and AS (in centimeters) are 15, 16, and 17 respectively, then the length of TC (in centimeters) is ______.
In ΔABC, if DE || BC, AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, then value of x is ______.
