Advertisements
Advertisements
प्रश्न
In an equilateral triangle ABC, the side BC is trisected at D. Prove that 9 AD2 = 7 AB2.
उत्तर

Let side of equilateral triangle be a. And AE be the altitude of ΔABC
So, BE = EC = `"BC"/(2) = "a"/(2)`
And, AE = `("a"sqrt(3))/(2)`
Given that BD = `(1)/(3)"BC" = "a"/(3)`
So, DE = BD - BE = `"a"/(2) - "a"/(3) = "a"/(6)`
Now, in ΔADE by applying Pythagoras theorem
AD2 = AE2 + DE2
AD2 = `(("a"sqrt(3))/(2))^2 + ("a"/6)^2`
= `((3"a"^2)/4) + ("a"^2/36) = (28"a"^2)/(36)`
Or, 9 AD2 = 7 AB2.
APPEARS IN
संबंधित प्रश्न
In Figure ABD is a triangle right angled at A and AC ⊥ BD. Show that AC2 = BC × DC

The perpendicular from A on side BC of a Δ ABC intersects BC at D such that DB = 3CD . Prove that 2AB2 = 2AC2 + BC2.

In the given figure, ABC is a triangle in which ∠ABC> 90° and AD ⊥ CB produced. Prove that AC2 = AB2 + BC2 + 2BC.BD.

For finding AB and BC with the help of information given in the figure, complete following activity.
AB = BC .......... 
∴ ∠BAC = 
∴ AB = BC =  × AC
× AC
=  × `sqrt8`
× `sqrt8`
=  × `2sqrt2`
× `2sqrt2`
= 

In the following Figure ∠ACB= 90° and CD ⊥ AB, prove that CD2 = BD × AD

Find the value of (sin2 33 + sin2 57°)
The sides of a certain triangle is given below. Find, which of them is right-triangle
16 cm, 20 cm, and 12 cm
Show that the triangle ABC is a right-angled triangle; if: AB = 9 cm, BC = 40 cm and AC = 41 cm
In the given figure, AD = 13 cm, BC = 12 cm, AB = 3 cm and angle ACD = angle ABC = 90°. Find the length of DC.

In the figure below, find the value of 'x'.
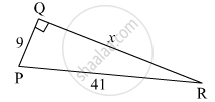
In the figure below, find the value of 'x'.

The sides of the triangle are given below. Find out which one is the right-angled triangle?
8, 15, 17
In a square PQRS of side 5 cm, A, B, C and D are points on sides PQ, QR, RS and SP respectively such as PA = PD = RB = RC = 2 cm. Prove that ABCD is a rectangle. Also, find the area and perimeter of the rectangle.
The hypotenuse of a right angled triangle of sides 12 cm and 16 cm is __________
The perimeters of two similar triangles ABC and PQR are 60 cm and 36 cm respectively. If PQ = 9 cm, then AB equals ______.
Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
If the hypotenuse of one right triangle is equal to the hypotenuse of another right triangle, then the triangles are congruent.
Points A and B are on the opposite edges of a pond as shown in figure. To find the distance between the two points, the surveyor makes a right-angled triangle as shown. Find the distance AB.

