Advertisements
Advertisements
प्रश्न
In a square PQRS of side 5 cm, A, B, C and D are points on sides PQ, QR, RS and SP respectively such as PA = PD = RB = RC = 2 cm. Prove that ABCD is a rectangle. Also, find the area and perimeter of the rectangle.
उत्तर
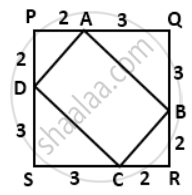
In ΔAPD, ∠P = 90°
∴ AD2 = AP2 + PD2
= 22 + 22
= 4 + 4
= 8
⇒ AD = `2sqrt(2)"cm"`
Similarly, we can prove that in ΔBRC,
BC = `2sqrt(2)"cm"`
∴ AD = BC ....(i)
In ΔAQB, ∠Q = 90°
∴ AB2 = AQ2 + BQ2
= 32 + 32
= 9 + 9
= 18
⇒ AB = `3sqrt(2)"cm"`
Similarly, we can prove that in ΔCSD,
CD = `3sqrt(2)"cm"`
∴ AB = CD ....(ii)
|Again, in ΔAPD,
AP = PD
⇒ ∠PAD = ∠PDA = 45°
Also, in ΔAQB,
AQ = BQ
⇒ ∠QAB = ∠QBA = 45°
Now, ∠PAD + ∠DAB + ∠QAB = 180°
⇒ 45° + ∠DAB + 45° = 180°
⇒ ∠DAB = 90°
Similarly, we can prove that ∠ABC, ∠BCD and ∠ADC are 90° each.
Thus, ABCD is a rectangle as opposite as opposite sides are equal and each angle is 90°.
Now,
Area of a rectangle ABCD
= AD x AB
= `2sqrt(2) xx 3sqrt(2)`
= 12cm2
Perimeter of a rectangle ABCD
= AB + BC + CD + AD
= `2sqrt(2) + 3sqrt(2) + 2sqrt(2) + 3sqrt(2)`
= `10sqrt(2)"cm"`.
APPEARS IN
संबंधित प्रश्न
ABCD is a rectangle whose three vertices are B (4, 0), C(4, 3) and D(0,3). The length of one of its diagonals is
(A) 5
(B) 4
(C) 3
(D) 25
A man goes 10 m due east and then 24 m due north. Find the distance from the starting point
Sides of triangles are given below. Determine it is a right triangles? In case of a right triangle, write the length of its hypotenuse. 3 cm, 8 cm, 6 cm
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
Prove that the points A(0, −1), B(−2, 3), C(6, 7) and D(8, 3) are the vertices of a rectangle ABCD?
In the given figure, ∠B = 90°, XY || BC, AB = 12 cm, AY = 8cm and AX : XB = 1 : 2 = AY : YC.
Find the lengths of AC and BC.

In triangle ABC, AB = AC = x, BC = 10 cm and the area of the triangle is 60 cm2.
Find x.
In the right-angled ∆LMN, ∠M = 90°. If l(LM) = 12 cm and l(LN) = 20 cm, find the length of seg MN.
Find the Pythagorean triplet from among the following set of numbers.
2, 6, 7
The sides of the triangle are given below. Find out which one is the right-angled triangle?
40, 20, 30
In an equilateral triangle ABC, the side BC is trisected at D. Prove that 9 AD2 = 7 AB2.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AC2 = AD2 + BC x DE + `(1)/(4)"BC"^2`
∆ABC is right-angled at C. If AC = 5 cm and BC = 12 cm. find the length of AB.
A man goes 18 m due east and then 24 m due north. Find the distance of his current position from the starting point?
In a right angled triangle, the hypotenuse is the greatest side
If ΔABC ~ ΔPQR, `("ar" triangle "ABC")/("ar" triangle "PQR") = 9/4` and AB = 18 cm, then the length of PQ is ______.
If two legs of a right triangle are equal to two legs of another right triangle, then the right triangles are congruent.
The hypotenuse (in cm) of a right angled triangle is 6 cm more than twice the length of the shortest side. If the length of third side is 6 cm less than thrice the length of shortest side, then find the dimensions of the triangle.
Jayanti takes shortest route to her home by walking diagonally across a rectangular park. The park measures 60 metres × 80 metres. How much shorter is the route across the park than the route around its edges?
