Advertisements
Advertisements
प्रश्न
A man goes 18 m due east and then 24 m due north. Find the distance of his current position from the starting point?
उत्तर
Let the initial position of the man be “O” and his final position be “B”.
By Pythagoras theorem
In the right ∆OAB,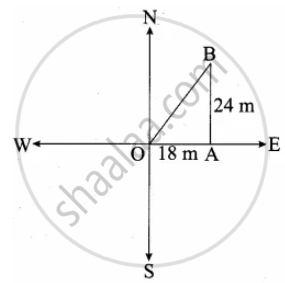
OB2 = OA2 + AB2
= 182 + 242
= 324 + 576 = 900
OB = `sqrt(900)` = 30
The distance of his current position is 30 m
APPEARS IN
संबंधित प्रश्न
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
In the given figure, ABC is a triangle in which ∠ABC < 90° and AD ⊥ BC. Prove that AC2 = AB2 + BC2 − 2BC.BD.

If the sides of the triangle are in the ratio 1: `sqrt2`: 1, show that is a right-angled triangle.
In triangle ABC, angle A = 90o, CA = AB and D is the point on AB produced.
Prove that DC2 - BD2 = 2AB.AD.
ABC is a triangle, right-angled at B. M is a point on BC.
Prove that: AM2 + BC2 = AC2 + BM2
In the figure below, find the value of 'x'.

In ΔABC, AD is perpendicular to BC. Prove that: AB2 + CD2 = AC2 + BD2
The hypotenuse of a right angled triangle of sides 12 cm and 16 cm is __________
If two legs of a right triangle are equal to two legs of another right triangle, then the right triangles are congruent.
The hypotenuse (in cm) of a right angled triangle is 6 cm more than twice the length of the shortest side. If the length of third side is 6 cm less than thrice the length of shortest side, then find the dimensions of the triangle.
