Advertisements
Advertisements
प्रश्न
If the sides of the triangle are in the ratio 1: `sqrt2`: 1, show that is a right-angled triangle.
उत्तर
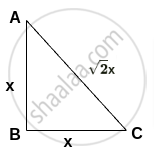
Let, the sides of the triangle be, x: `sqrt2`x and x.
AB2 + BC2 = x2 +x2 = 2x2
AC2 = `(sqrt2 x)^2` = 2x2
AB2 + BC2 = AC2
Conversely, if in any triangle, the square on the largest side of the triangle is equal to the sum of the squares on remaining two sides, then the triangle is a right-angled triangle and the angle opposite to the largest side is a right-angle.
Therefore, Δ ABC is a right-angled triangle.
APPEARS IN
संबंधित प्रश्न
In a right triangle ABC, right-angled at B, BC = 12 cm and AB = 5 cm. The radius of the circle inscribed in the triangle (in cm) is
(A) 4
(B) 3
(C) 2
(D) 1
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 50 cm, 80 cm, 100 cm
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 13 cm, 12 cm, 5 cm
An aeroplane leaves an airport and flies due north at a speed of 1,000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1,200 km per hour. How far apart will be the two planes after `1 1/2` hours?
The perpendicular from A on side BC of a Δ ABC intersects BC at D such that DB = 3CD . Prove that 2AB2 = 2AC2 + BC2.

In ∆ABC, AB = 10, AC = 7, BC = 9, then find the length of the median drawn from point C to side AB.
In an isosceles triangle, length of the congruent sides is 13 cm and its base is 10 cm. Find the distance between the vertex opposite the base and the centroid.
In triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC.

Choose the correct alternative:
In right-angled triangle PQR, if hypotenuse PR = 12 and PQ = 6, then what is the measure of ∠P?
Each side of rhombus is 10cm. If one of its diagonals is 16cm, find the length of the other diagonals.
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = AE2 + CD2 + BF2
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
In a square PQRS of side 5 cm, A, B, C and D are points on sides PQ, QR, RS and SP respectively such as PA = PD = RB = RC = 2 cm. Prove that ABCD is a rectangle. Also, find the area and perimeter of the rectangle.
∆ABC is right-angled at C. If AC = 5 cm and BC = 12 cm. find the length of AB.
Find the unknown side in the following triangles
Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
Two squares having same perimeter are congruent.
If two legs of a right triangle are equal to two legs of another right triangle, then the right triangles are congruent.
If the hypotenuse of one right triangle is equal to the hypotenuse of another right triangle, then the triangles are congruent.
