Advertisements
Advertisements
प्रश्न
In ∆ABC, AB = 10, AC = 7, BC = 9, then find the length of the median drawn from point C to side AB.
उत्तर
Let CD be the median drawn from the vertex C to side AB.
`"BD" = 1/2 × "AB"` ...(D is the midpoint of AB)
∴ BD = `1/2 × 10`
∴ BD = 5 units

In ∆ABC,
seg CD is the median. ...(Given)
By Apollonius theorem,
∴ AC2 + BC2 = 2CD2 + 2BD2
∴ 72 + 92 = 2CD2 + 2(5)2
∴ 49 + 81 = 2CD2 + 2 × 25
∴ 130 = 2CD2 + 50
∴ 2CD2 = 130 − 50
∴ CD2 = `80/2`
संबंधित प्रश्न
Prove that the diagonals of a rectangle ABCD, with vertices A(2, -1), B(5, -1), C(5, 6) and D(2, 6), are equal and bisect each other.
From a point O in the interior of a ∆ABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove
that :
`(i) AF^2 + BD^2 + CE^2 = OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2`
`(ii) AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2`
In Figure ABD is a triangle right angled at A and AC ⊥ BD. Show that AC2 = BC × DC

A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2 + BD2 = AB2 + DE2
Identify, with reason, if the following is a Pythagorean triplet.
(10, 24, 27)
Identify, with reason, if the following is a Pythagorean triplet.
(11, 60, 61)
In right angle ΔABC, if ∠B = 90°, AB = 6, BC = 8, then find AC.
In triangle ABC, AB = AC and BD is perpendicular to AC.
Prove that: BD2 - CD2 = 2CD × AD
In the given figure, BL and CM are medians of a ∆ABC right-angled at A. Prove that 4 (BL2 + CM2) = 5 BC2.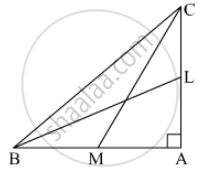
The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 60, 61
A right triangle has hypotenuse p cm and one side q cm. If p - q = 1, find the length of third side of the triangle.
In a square PQRS of side 5 cm, A, B, C and D are points on sides PQ, QR, RS and SP respectively such as PA = PD = RB = RC = 2 cm. Prove that ABCD is a rectangle. Also, find the area and perimeter of the rectangle.
A man goes 18 m due east and then 24 m due north. Find the distance of his current position from the starting point?
If in a ΔPQR, PR2 = PQ2 + QR2, then the right angle of ∆PQR is at the vertex ________
Find the unknown side in the following triangles
In a right angled triangle, if length of hypotenuse is 25 cm and height is 7 cm, then what is the length of its base?
If the areas of two circles are the same, they are congruent.
Two circles having same circumference are congruent.
