Advertisements
Advertisements
प्रश्न
Prove that the diagonals of a rectangle ABCD, with vertices A(2, -1), B(5, -1), C(5, 6) and D(2, 6), are equal and bisect each other.
उत्तर १
Solution:
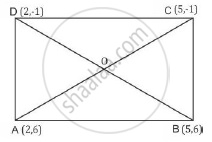
ΔADC and ΔBDC are right angled triangles with AD and BC as hypotaneus
`AC^2=BA^2+BC^2`
`AC^2=(5-2)^2+(6+1)^2=9+49=58 sq.unit`
`BD^2=DC^2+CB^2`
`BD^2=(5-2)^2+(-1-6)^2=9+49=58 sq.unit`
Hence, both the diagonals are equal in length.
उत्तर २
The vertices of the rectangle ABCD are A(2, -1), B(5, -1), C(5, 6) and D(2, 6) Now,
`"Coordinates of midpoint of" AC = ((2+5)/2 , (-1+6)/2) = (7/5 ,5/2)`
`"Coordinates of midpoint of " BD = ((5+2)/2 , (-1+6)/2)= (7/2,5/2)`
Since, the midpoints of AC and BD coincide, therefore the diagonals of rectangle ABCD bisect each other.
संबंधित प्रश्न
Two towers of heights 10 m and 30 m stand on a plane ground. If the distance between their feet is 15 m, find the distance between their tops
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 50 cm, 80 cm, 100 cm
In an isosceles triangle, length of the congruent sides is 13 cm and its base is 10 cm. Find the distance between the vertex opposite the base and the centroid.
In ΔABC, Find the sides of the triangle, if:
- AB = ( x - 3 ) cm, BC = ( x + 4 ) cm and AC = ( x + 6 ) cm
- AB = x cm, BC = ( 4x + 4 ) cm and AC = ( 4x + 5) cm
In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
Prove that: 2AC2 - AB2 = BC2 + CD2 + DA2
Find the length of the hypotenuse of a triangle whose other two sides are 24cm and 7cm.
A right triangle has hypotenuse p cm and one side q cm. If p - q = 1, find the length of third side of the triangle.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AC2 - AB2 = 2BC x ED
Find the unknown side in the following triangles
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its top reach?
