Advertisements
Advertisements
Question
Prove that the diagonals of a rectangle ABCD, with vertices A(2, -1), B(5, -1), C(5, 6) and D(2, 6), are equal and bisect each other.
Solution 1
Solution:
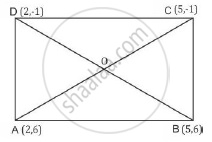
ΔADC and ΔBDC are right angled triangles with AD and BC as hypotaneus
`AC^2=BA^2+BC^2`
`AC^2=(5-2)^2+(6+1)^2=9+49=58 sq.unit`
`BD^2=DC^2+CB^2`
`BD^2=(5-2)^2+(-1-6)^2=9+49=58 sq.unit`
Hence, both the diagonals are equal in length.
Solution 2
The vertices of the rectangle ABCD are A(2, -1), B(5, -1), C(5, 6) and D(2, 6) Now,
`"Coordinates of midpoint of" AC = ((2+5)/2 , (-1+6)/2) = (7/5 ,5/2)`
`"Coordinates of midpoint of " BD = ((5+2)/2 , (-1+6)/2)= (7/2,5/2)`
Since, the midpoints of AC and BD coincide, therefore the diagonals of rectangle ABCD bisect each other.
RELATED QUESTIONS
From a point O in the interior of a ∆ABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove
that :
`(i) AF^2 + BD^2 + CE^2 = OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2`
`(ii) AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2`
ABC is an isosceles triangle with AC = BC. If AB2 = 2AC2, prove that ABC is a right triangle.
For finding AB and BC with the help of information given in the figure, complete following activity.
AB = BC .......... 
∴ ∠BAC = 
∴ AB = BC =  × AC
× AC
=  × `sqrt8`
× `sqrt8`
=  × `2sqrt2`
× `2sqrt2`
= 

In ∆PQR, point S is the midpoint of side QR. If PQ = 11, PR = 17, PS = 13, find QR.
The given figure shows a quadrilateral ABCD in which AD = 13 cm, DC = 12 cm, BC = 3 cm and ∠ABD = ∠BCD = 90o. Calculate the length of AB.
In figure AB = BC and AD is perpendicular to CD.
Prove that: AC2 = 2BC. DC.
In the given figure, angle BAC = 90°, AC = 400 m, and AB = 300 m. Find the length of BC.

Find the Pythagorean triplet from among the following set of numbers.
3, 4, 5
Find the unknown side in the following triangles
Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
