Advertisements
Advertisements
प्रश्न
Prove that the diagonals of a rectangle ABCD, with vertices A(2, -1), B(5, -1), C(5, 6) and D(2, 6), are equal and bisect each other.
उत्तर १
Solution:
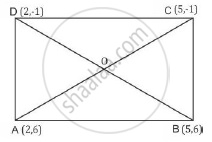
ΔADC and ΔBDC are right angled triangles with AD and BC as hypotaneus
`AC^2=BA^2+BC^2`
`AC^2=(5-2)^2+(6+1)^2=9+49=58 sq.unit`
`BD^2=DC^2+CB^2`
`BD^2=(5-2)^2+(-1-6)^2=9+49=58 sq.unit`
Hence, both the diagonals are equal in length.
उत्तर २
The vertices of the rectangle ABCD are A(2, -1), B(5, -1), C(5, 6) and D(2, 6) Now,
`"Coordinates of midpoint of" AC = ((2+5)/2 , (-1+6)/2) = (7/5 ,5/2)`
`"Coordinates of midpoint of " BD = ((5+2)/2 , (-1+6)/2)= (7/2,5/2)`
Since, the midpoints of AC and BD coincide, therefore the diagonals of rectangle ABCD bisect each other.
संबंधित प्रश्न
If ABC is an equilateral triangle of side a, prove that its altitude = ` \frac { \sqrt { 3 } }{ 2 } a`
ABC is a right-angled triangle, right-angled at A. A circle is inscribed in it. The lengths of the two sides containing the right angle are 5 cm and 12 cm. Find the radius of the circle
In the given figure, ABC is a triangle in which ∠ABC> 90° and AD ⊥ CB produced. Prove that AC2 = AB2 + BC2 + 2BC.BD.

In the given figure, ∆ABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices ?

In ΔABC, Find the sides of the triangle, if:
- AB = ( x - 3 ) cm, BC = ( x + 4 ) cm and AC = ( x + 6 ) cm
- AB = x cm, BC = ( 4x + 4 ) cm and AC = ( 4x + 5) cm
Two poles of heights 6 m and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m;
find the distance between their tips.
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2 ) = (AB2 + PQ2)
In the given figure, BL and CM are medians of a ∆ABC right-angled at A. Prove that 4 (BL2 + CM2) = 5 BC2.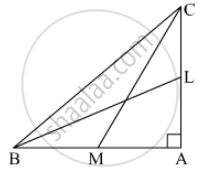
Each side of rhombus is 10cm. If one of its diagonals is 16cm, find the length of the other diagonals.
In a triangle, sum of squares of two sides is equal to the square of the third side.
