Advertisements
Advertisements
प्रश्न
In the given figure, BL and CM are medians of a ∆ABC right-angled at A. Prove that 4 (BL2 + CM2) = 5 BC2.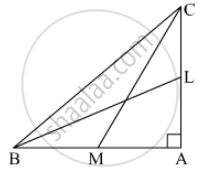
उत्तर
To prove: 4(BL2 + CM2 ) = 5BC2
Proof: In ΔCAB,
Applying Pythagoras theorem,
AB2 + AC2 = BC2 .....(1)
In ΔABL,
AL2 + AB2 = BL2
⇒ `("AC"/2)^2 + "AB"^2 = "BL"^2`
⇒ `"AC"^2 + 4"AB"^2 = 4"BL"^2` .....(2)
In ΔCAM,
CA2 + MA2 = CM2
⇒ `(("BA")/2)^2`+ CA2 = CM2
⇒ BA2 + 4CA2 = 4CM2 .....(3)
Adding (2) and (3)
AC2 + 4AB2 + BA2 + 4CA2 = 4BL2 + 4CM2
⇒ 5AC2 + 5AB2 = 4(BL2 + CM2)
⇒ 5(AC2 + AB2) = 4(BL2 + CM2)
⇒ 5(BC2) = 4(BL2 + CM2) ....( From 1 )
Hence Proved.
संबंधित प्रश्न
P and Q are the mid-points of the sides CA and CB respectively of a ∆ABC, right angled at C. Prove that:
`(i) 4AQ^2 = 4AC^2 + BC^2`
`(ii) 4BP^2 = 4BC^2 + AC^2`
`(iii) (4AQ^2 + BP^2 ) = 5AB^2`
From a point O in the interior of a ∆ABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove
that :
`(i) AF^2 + BD^2 + CE^2 = OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2`
`(ii) AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2`
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
In ∆ABC, seg AD ⊥ seg BC, DB = 3CD.
Prove that: 2AB2 = 2AC2 + BC2

If the angles of a triangle are 30°, 60°, and 90°, then shown that the side opposite to 30° is half of the hypotenuse, and the side opposite to 60° is `sqrt(3)/2` times of the hypotenuse.
Find the value of (sin2 33 + sin2 57°)
In an equilateral triangle ABC, the side BC is trisected at D. Prove that 9 AD2 = 7 AB2.
Choose the correct alternative:
If length of sides of a triangle are a, b, c and a2 + b2 = c2, then which type of triangle it is?
In ΔABC, if DE || BC, AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, then value of x is ______.
Two trees 7 m and 4 m high stand upright on a ground. If their bases (roots) are 4 m apart, then the distance between their tops is ______.
