Advertisements
Advertisements
प्रश्न
In the given figure, BL and CM are medians of a ∆ABC right-angled at A. Prove that 4 (BL2 + CM2) = 5 BC2.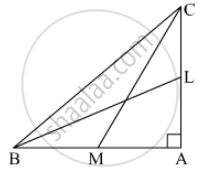
उत्तर
To prove: 4(BL2 + CM2 ) = 5BC2
Proof: In ΔCAB,
Applying Pythagoras theorem,
AB2 + AC2 = BC2 .....(1)
In ΔABL,
AL2 + AB2 = BL2
⇒ `("AC"/2)^2 + "AB"^2 = "BL"^2`
⇒ `"AC"^2 + 4"AB"^2 = 4"BL"^2` .....(2)
In ΔCAM,
CA2 + MA2 = CM2
⇒ `(("BA")/2)^2`+ CA2 = CM2
⇒ BA2 + 4CA2 = 4CM2 .....(3)
Adding (2) and (3)
AC2 + 4AB2 + BA2 + 4CA2 = 4BL2 + 4CM2
⇒ 5AC2 + 5AB2 = 4(BL2 + CM2)
⇒ 5(AC2 + AB2) = 4(BL2 + CM2)
⇒ 5(BC2) = 4(BL2 + CM2) ....( From 1 )
Hence Proved.
संबंधित प्रश्न
A ladder leaning against a wall makes an angle of 60° with the horizontal. If the foot of the ladder is 2.5 m away from the wall, find the length of the ladder
From a point O in the interior of a ∆ABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove
that :
`(i) AF^2 + BD^2 + CE^2 = OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2`
`(ii) AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2`
An aeroplane leaves an airport and flies due north at a speed of 1,000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1,200 km per hour. How far apart will be the two planes after `1 1/2` hours?
In triangle ABC, AB = AC and BD is perpendicular to AC.
Prove that: BD2 - CD2 = 2CD × AD
In figure AB = BC and AD is perpendicular to CD.
Prove that: AC2 = 2BC. DC.
ABC is a triangle, right-angled at B. M is a point on BC.
Prove that: AM2 + BC2 = AC2 + BM2
O is any point inside a rectangle ABCD.
Prove that: OB2 + OD2 = OC2 + OA2.
In a rectangle ABCD,
prove that: AC2 + BD2 = AB2 + BC2 + CD2 + DA2.
In the given figure, angle BAC = 90°, AC = 400 m, and AB = 300 m. Find the length of BC.

In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
