Question

From a point O in the interior of a ∆ABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove
that :

`(i) AF^2 + BD^2 + CE^2 = OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2`

`(ii) AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2`

Answer 1

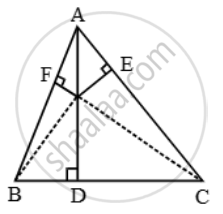
Let O be a point in the interior of ∆ABC and let OD ⊥ BC, OE ⊥ CA and OF ⊥ AB.

(i) In right triangles ∆OFA, ∆ODB and ∆OEC, we have

`OA^2 = AF^2 + OF^2`

`OB^2 = BD^2 + OD^2`

and,

`OC^2 = CE^2 + OE^2`

Adding all these results, we get

`OA^2 + OB^2 + OC^2 = AF^2 + BD^2 + CE^2 + OF^2 + OD^2 + OE^2`

`⇒ AF^2 + BD^2 + CE^2 = OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2`

(ii) In right triangles ∆ODB and ∆ODC, we have

`OB^2 = OD^2 + BD^2`

and, `OC^2 = OD^2 + CD^2`

`OB^2 – OC^2 = (OD^2 + BD^2 ) – (OD^2 + CD^2 )`

`⇒ OB^2 – OC^2 = BD^2 – CD^2 ….(i)`

Similarly, we have

`OC^2 – OA^2 = CE^2 – AE^2 ….(ii)`

and, `OA^2 – OB^2 = AF^2 – BF^2 ….(iii)`

Adding (i), (ii) and (iii), we get

`(OB^2 – OC^2 ) + (OC^2 – OA^2 ) + (OA^2 – OB^2 )`

`= (BD^2 – CD^2 ) + (CE^2 – AE^2 ) + (AF^2 – BF^2 )`

`⇒ (BD^2 + CE^2 + AF^2 ) – (AE^2 + CD^2 + BF^2 ) = 0`

`⇒ AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2`