Advertisements
Advertisements
प्रश्न
An aeroplane leaves an airport and flies due north at a speed of 1,000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1,200 km per hour. How far apart will be the two planes after `1 1/2` hours?
उत्तर
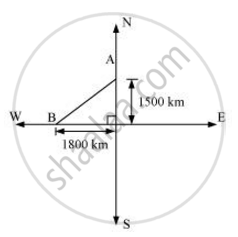
Distance travelled by the plane flying towards north in `1 1/2 `
Similarly, distance travelled by the plane flying towards west in `1 1/2 `
Let these distances be represented by OA and OB respectively.
Applying Pythagoras theorem,
Distance between these planes after `1 1/2 `
`= (sqrt((1500)^2 + (1800)^2)) `
`= (sqrt5490000)`
Therefore, the distance between these planes will be `300sqrt(61) `
APPEARS IN
संबंधित प्रश्न
ABC is an isosceles triangle with AC = BC. If AB2 = 2AC2, prove that ABC is a right triangle.
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.

In the given figure, ∠B = 90°, XY || BC, AB = 12 cm, AY = 8cm and AX : XB = 1 : 2 = AY : YC.
Find the lengths of AC and BC.

In an isosceles triangle ABC; AB = AC and D is the point on BC produced.
Prove that: AD2 = AC2 + BD.CD.
In a rectangle ABCD,
prove that: AC2 + BD2 = AB2 + BC2 + CD2 + DA2.
M andN are the mid-points of the sides QR and PQ respectively of a PQR, right-angled at Q.
Prove that:
(i) PM2 + RN2 = 5 MN2
(ii) 4 PM2 = 4 PQ2 + QR2
(iii) 4 RN2 = PQ2 + 4 QR2(iv) 4 (PM2 + RN2) = 5 PR2
In triangle PQR, angle Q = 90°, find: PQ, if PR = 34 cm and QR = 30 cm
Find the Pythagorean triplet from among the following set of numbers.
3, 4, 5
