Advertisements
Advertisements
प्रश्न
An aeroplane leaves an airport and flies due north at a speed of 1,000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1,200 km per hour. How far apart will be the two planes after `1 1/2` hours?
उत्तर
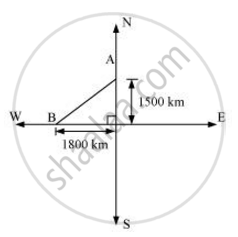
Distance travelled by the plane flying towards north in `1 1/2 `
Similarly, distance travelled by the plane flying towards west in `1 1/2 `
Let these distances be represented by OA and OB respectively.
Applying Pythagoras theorem,
Distance between these planes after `1 1/2 `
`= (sqrt((1500)^2 + (1800)^2)) `
`= (sqrt5490000)`
Therefore, the distance between these planes will be `300sqrt(61) `
APPEARS IN
संबंधित प्रश्न
In triangle ABC, ∠C=90°. Let BC= a, CA= b, AB= c and let 'p' be the length of the perpendicular from 'C' on AB, prove that:
1. cp = ab
2. `1/p^2=1/a^2+1/b^2`
ABCD is a rectangle whose three vertices are B (4, 0), C(4, 3) and D(0,3). The length of one of its diagonals is
(A) 5
(B) 4
(C) 3
(D) 25
ABC is a right-angled triangle, right-angled at A. A circle is inscribed in it. The lengths of the two sides containing the right angle are 5 cm and 12 cm. Find the radius of the circle
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals
The perimeter of a triangle with vertices (0, 4), (0, 0) and (3, 0) is
(A)\[7 + \sqrt{5}\]
(B) 5
(C) 10
(D) 12
Some question and their alternative answer are given. Select the correct alternative.
If a, b, and c are sides of a triangle and a2 + b2 = c2, name the type of triangle.
In the following Figure ∠ACB= 90° and CD ⊥ AB, prove that CD2 = BD × AD

In Fig. 3, ∠ACB = 90° and CD ⊥ AB, prove that CD2 = BD x AD.

In the given figure, angle BAC = 90°, AC = 400 m, and AB = 300 m. Find the length of BC.

In a right angled triangle, if length of hypotenuse is 25 cm and height is 7 cm, then what is the length of its base?
