Advertisements
Advertisements
प्रश्न
A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?
उत्तर
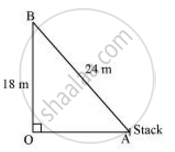
Let OB be the pole and AB be the wire.
By Pythagoras theorem,
AB2 = OB2 + OA2
(24m)2 = (18m)2 + OA2
OA2 = (576 - 324)m2 = 25 m2
OA2 = `sqrt252 `
Therefore, the distance from the base is `6sqrt7 m`
संबंधित प्रश्न
Sides of triangles are given below. Determine it is a right triangles? In case of a right triangle, write the length of its hypotenuse. 3 cm, 8 cm, 6 cm
In the given figure, point T is in the interior of rectangle PQRS, Prove that, TS2 + TQ2 = TP2 + TR2 (As shown in the figure, draw seg AB || side SR and A-T-B)


In ΔMNP, ∠MNP = 90˚, seg NQ ⊥ seg MP, MQ = 9, QP = 4, find NQ.
In triangle ABC, ∠B = 90o and D is the mid-point of BC.
Prove that: AC2 = AD2 + 3CD2.
Choose the correct alternative:
In right-angled triangle PQR, if hypotenuse PR = 12 and PQ = 6, then what is the measure of ∠P?
Prove that (1 + cot A - cosec A ) (1 + tan A + sec A) = 2
In the figure below, find the value of 'x'.

A ladder 25m long reaches a window of a building 20m above the ground. Determine the distance of the foot of the ladder from the building.
Find the unknown side in the following triangles
In a right-angled triangle ABC, if angle B = 90°, BC = 3 cm and AC = 5 cm, then the length of side AB is ______.
