Advertisements
Advertisements
प्रश्न
In the given figure, point T is in the interior of rectangle PQRS, Prove that, TS2 + TQ2 = TP2 + TR2 (As shown in the figure, draw seg AB || side SR and A-T-B)
Advertisements
उत्तर १
Construction: Through T, draw seg AB II side SR such that A-T-B, P- A-S and Q-B-R.
Proof:
seg PS || seg QR ...(Opposite sides of rectangle)
∴ seg AS || seg BR ...(P-A-S and Q-B-R)
also seg AB || seg SR ...(Construction)
∴ `square` ASRB is a parallelogram ...((By definition)
∠ASR = 90° ...(Angle of rectangle PSRQ)
∴ `square` ASRB is a rectangle ...(A parallelogram is a rectangle, if one of its angles is a right angle.)
∠SAB = ∠ABR = 90° ...(Angle of a rectangle)
∴ seg TA ⊥ side PS and seg TB ⊥ side QR ...(1)
AS = BR ...(2) (Opposite sides of rectangle are equal)
Similarly, we can prove AP= BQ ...(3)
In ΔTAS,
∠TAS = 90° ...[From (1)]
∴ by Pythagoras theorem,
TS2 = TA2 + AS2 ...(4)
In ΔTBQ,
∠TBQ = 90° ...[From (1)]
∴ by Pythagoras theorem,
TQ2 = TB2 + BQ2 ...(5)
Adding (4) and (5), we get,
TS2 + TQ2 = TA2 + AS2 + TB2 + BQ2 ...(6)
In ΔTAP,
∠TAP = 90° ...[From (1)]
∴ by Pythagoras theorem,
TP2 = TA2 + AP2 ...(7)
In ΔTBR,
∠TBR = 90° ...[From (1)]
∴ by Pythagoras theorem,
TR2 = TB2 + BR2 ...(8)
Adding (7) and (8), we get
TP2 + TR2 = TA2 + AP2 + TB2 + BR2
∴ TP2 + TR2 = TA2 + BQ2 + TB2 + AS2 ...(9) [From (2) and (3)]
∴ from (6) and (g), we get,
TS2 + TQ2 = TP2 + TR2
उत्तर २
Construction: Draw diagonals PR and QS and let them intersect at 0. Draw seg TO.
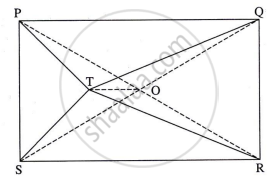
Proof: `square` PQRS is a rectangle ...(Given)
∴ PR=QS ...(Diagonals of rectangle are congruent)
Multiplying both the sides by `1/2`, we get,
`1/2`PR = `1/2`QS ...(1)
But, `1/2`PR = OP = OR ...(2)
and `1/2`QS = OS = OQ ...(3) [Diagonals of rectangle bisect each other]
∴ OP = OR = OS = OQ ...(4) [From (1), (2) and (3)]
In ΔTSQ,
seg TO is the median ...(By definition)
∴ by Apollonius theorem,
TS2 + TQ2 = 2TO2 + 2OQ2 ...(5)
In ΔPTR,
seg TO is the median ...(By definition)
∴ by Apollonius theorem,
TP2 + TR2 = 2TO2 + 2OR2
∴ TP2 + TR2 = 2TO2 + 2OQ2 ...(6) [From (4)]
∴ from (5) and (6), we get,
TS2 + TQ2 = TP2 + TR2
Notes
Students can refer to the provided solutions based on their preferred marks.
संबंधित प्रश्न
In Fig., ∆ABC is an obtuse triangle, obtuse angled at B. If AD ⊥ CB, prove that AC2 = AB2 + BC2 + 2BC × BD
Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
Prove that the points A(0, −1), B(−2, 3), C(6, 7) and D(8, 3) are the vertices of a rectangle ABCD?
Identify, with reason, if the following is a Pythagorean triplet.
(5, 12, 13)
For finding AB and BC with the help of information given in the figure, complete following activity.
AB = BC .......... 
∴ ∠BAC =
∴ AB = BC = × AC
= × `sqrt8`
= × `2sqrt2`
=
Some question and their alternative answer are given. Select the correct alternative.
If a, b, and c are sides of a triangle and a2 + b2 = c2, name the type of triangle.
In triangle ABC, AB = AC and BD is perpendicular to AC.
Prove that: BD2 − CD2 = 2CD × AD
The sides of the triangle are given below. Find out which one is the right-angled triangle?
8, 15, 17
The sides of the triangle are given below. Find out which one is the right-angled triangle?
1.5, 1.6, 1.7
A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
In an equilateral triangle ABC, the side BC is trisected at D. Prove that 9 AD2 = 7 AB2.
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = AE2 + CD2 + BF2
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2(AD2 + CD2)
If ‘l‘ and ‘m’ are the legs and ‘n’ is the hypotenuse of a right angled triangle then, l2 = ________
In triangle ABC, line I, is a perpendicular bisector of BC.
If BC = 12 cm, SM = 8 cm, find CS
In the given figure, ∠T and ∠B are right angles. If the length of AT, BC and AS (in centimeters) are 15, 16, and 17 respectively, then the length of TC (in centimeters) is ______.
Sides AB and BE of a right triangle, right-angled at B are of lengths 16 cm and 8 cm respectively. The length of the side of largest square FDGB that can be inscribed in the triangle ABE is ______.
Prove that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
Lengths of sides of a triangle are 3 cm, 4 cm and 5 cm. The triangle is ______.
Height of a pole is 8 m. Find the length of rope tied with its top from a point on the ground at a distance of 6 m from its bottom.
