Advertisements
Advertisements
प्रश्न
In a rectangle ABCD,
prove that: AC2 + BD2 = AB2 + BC2 + CD2 + DA2.
उत्तर
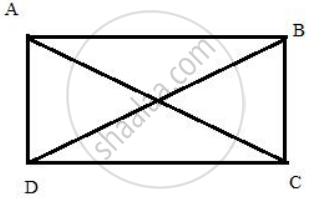
Pythagoras theorem states that in a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
Since, ABCD is a rectangle angles A, B, C and D are rt. angles.
First, we consider the ΔACD, and applying Pythagoras theorem we get,
AC2 = DA2 + CD2 ....(i)
Similarly, we get from rt. angle triangle BDC we get,
BD2 = BC2 + CD2
= BC2 + AB2 ....[ In a rectangle, opposite sides are equal, ∴ CD = AB ] ...(ii)
Adding (i) and (ii)
AC2 + BD2 = AB2 + BC2 + CD2 + DA2
Hence proved.
APPEARS IN
संबंधित प्रश्न
ABC is a triangle right angled at C. If AB = 25 cm and AC = 7 cm, find BC.
Which of the following can be the sides of a right triangle?
1.5 cm, 2 cm, 2.5 cm
In the case of right-angled triangles, identify the right angles.
In the given figure, M is the midpoint of QR. ∠PRQ = 90°. Prove that, PQ2 = 4PM2 – 3PR2.

Pranali and Prasad started walking to the East and to the North respectively, from the same point and at the same speed. After 2 hours distance between them was \[15\sqrt{2}\]
km. Find their speed per hour.
In right angle ΔABC, if ∠B = 90°, AB = 6, BC = 8, then find AC.
In an isosceles triangle ABC; AB = AC and D is the point on BC produced.
Prove that: AD2 = AC2 + BD.CD.
Diagonals of rhombus ABCD intersect each other at point O.
Prove that: OA2 + OC2 = 2AD2 - `"BD"^2/2`
In the following Figure ∠ACB= 90° and CD ⊥ AB, prove that CD2 = BD × AD

In Fig. 3, ∠ACB = 90° and CD ⊥ AB, prove that CD2 = BD x AD.

If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2 ) = (AB2 + PQ2)
Triangle ABC is right-angled at vertex A. Calculate the length of BC, if AB = 18 cm and AC = 24 cm.
Find the length of the hypotenuse of a triangle whose other two sides are 24cm and 7cm.
A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
Each side of rhombus is 10cm. If one of its diagonals is 16cm, find the length of the other diagonals.
In a right-angled triangle ABC,ABC = 90°, AC = 10 cm, BC = 6 cm and BC produced to D such CD = 9 cm. Find the length of AD.
There are two paths that one can choose to go from Sarah’s house to James's house. One way is to take C street, and the other way requires to take B street and then A street. How much shorter is the direct path along C street?

Find the distance between the helicopter and the ship
Lengths of sides of a triangle are 3 cm, 4 cm and 5 cm. The triangle is ______.
Two squares are congruent, if they have same ______.
Height of a pole is 8 m. Find the length of rope tied with its top from a point on the ground at a distance of 6 m from its bottom.
