Advertisements
Advertisements
प्रश्न
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = OA2 + OB2 + OC2 - OD2 - OE2 - OF2
उत्तर
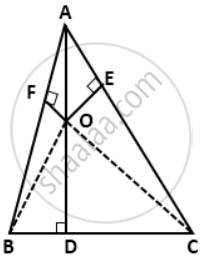
In right triangle OFA, ODB and OEC, we have
OA2 = AF2 + OF2
OB2 = BD2 + OD2
OC2 = CE2 + OE2
Adding all these results, we get
OA2 + OB2 + OC2 = AF2 + BD2 + CE2 + OF2 + OD2 + OE2
⇒ AF2 + BD2 + CE2 = OA2 + OB2 + OC2 - OD2 - OE2 - OF2.
APPEARS IN
संबंधित प्रश्न
Tick the correct answer and justify: In ΔABC, AB = `6sqrt3` cm, AC = 12 cm and BC = 6 cm.
The angle B is:
In the given figure, AD is a median of a triangle ABC and AM ⊥ BC. Prove that:

`"AC"^2 = "AD"^2 + "BC"."DM" + (("BC")/2)^2`
Prove that, in a right-angled triangle, the square of the hypotenuse is equal to the sum of the square of remaining two sides
In the given figure, ∆ABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices ?

For finding AB and BC with the help of information given in the figure, complete following activity.
AB = BC .......... 
∴ ∠BAC = 
∴ AB = BC =  × AC
× AC
=  × `sqrt8`
× `sqrt8`
=  × `2sqrt2`
× `2sqrt2`
= 

In the given figure, M is the midpoint of QR. ∠PRQ = 90°. Prove that, PQ2 = 4PM2 – 3PR2.

In right angle ΔABC, if ∠B = 90°, AB = 6, BC = 8, then find AC.
Find the length of diagonal of the square whose side is 8 cm.
In the given figure, angle ADB = 90°, AC = AB = 26 cm and BD = DC. If the length of AD = 24 cm; find the length of BC.

In an equilateral triangle ABC, the side BC is trisected at D. Prove that 9 AD2 = 7 AB2.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2AD2 + `(1)/(2)"BC"^2`
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2(AD2 + CD2)
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that: 9BP2 = 9BC2 + 4AC2
In the given figure, PQ = `"RS"/(3)` = 8cm, 3ST = 4QT = 48cm.
SHow that ∠RTP = 90°.
Find the unknown side in the following triangles
Find the distance between the helicopter and the ship
For going to a city B from city A, there is a route via city C such that AC ⊥ CB, AC = 2x km and CB = 2(x + 7) km. It is proposed to construct a 26 km highway which directly connects the two cities A and B. Find how much distance will be saved in reaching city B from city A after the construction of the highway.
In a quadrilateral ABCD, ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2
[Hint: Produce AB and DC to meet at E.]
If the areas of two circles are the same, they are congruent.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. Find the length of the ladder.
