Advertisements
Advertisements
प्रश्न
Find the length of diagonal of the square whose side is 8 cm.
उत्तर
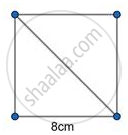
Length of the Diagonal
⇒
APPEARS IN
संबंधित प्रश्न
If the sides of a triangle are 6 cm, 8 cm and 10 cm, respectively, then determine whether the triangle is a right angle triangle or not.
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AB2 = BC × BD

Which of the following can be the sides of a right triangle?
2 cm, 2 cm, 5 cm
In the case of right-angled triangles, identify the right angles.
Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.
In right angle ΔABC, if ∠B = 90°, AB = 6, BC = 8, then find AC.
In ΔABC, Find the sides of the triangle, if:
- AB = ( x - 3 ) cm, BC = ( x + 4 ) cm and AC = ( x + 6 ) cm
- AB = x cm, BC = ( 4x + 4 ) cm and AC = ( 4x + 5) cm
ABC is a triangle, right-angled at B. M is a point on BC.
Prove that: AM2 + BC2 = AC2 + BM2
M andN are the mid-points of the sides QR and PQ respectively of a PQR, right-angled at Q.
Prove that:
(i) PM2 + RN2 = 5 MN2
(ii) 4 PM2 = 4 PQ2 + QR2
(iii) 4 RN2 = PQ2 + 4 QR2(iv) 4 (PM2 + RN2) = 5 PR2
Prove that (1 + cot A - cosec A ) (1 + tan A + sec A) = 2
In triangle PQR, angle Q = 90°, find: PR, if PQ = 8 cm and QR = 6 cm
The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 60, 61
A right triangle has hypotenuse p cm and one side q cm. If p - q = 1, find the length of third side of the triangle.
In the given figure, PQ =
SHow that ∠RTP = 90°.
In a right angled triangle, the hypotenuse is the greatest side
Find the unknown side in the following triangles
In a right angled triangle, if length of hypotenuse is 25 cm and height is 7 cm, then what is the length of its base?
In an isosceles triangle PQR, the length of equal sides PQ and PR is 13 cm and base QR is 10 cm. Find the length of perpendicular bisector drawn from vertex P to side QR.
If the hypotenuse of one right triangle is equal to the hypotenuse of another right triangle, then the triangles are congruent.
Two poles of 10 m and 15 m stand upright on a plane ground. If the distance between the tops is 13 m, find the distance between their feet.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its top reach?
