Advertisements
Advertisements
प्रश्न
Two poles of 10 m and 15 m stand upright on a plane ground. If the distance between the tops is 13 m, find the distance between their feet.
उत्तर
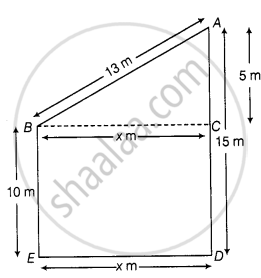
Let BC = x m
In right-angled ΔACB,
AB2 = AC2 + BC2 ......[By Pythagoras theorem]
⇒ (13)2 = (5)2 + x2
⇒ 169 – 25 = x2
⇒ 144 = x2
⇒ x = `sqrt(144)`
⇒ x = 12 m
Hence, the distance between the feet of two poles is 12 m.
APPEARS IN
संबंधित प्रश्न
ABCD is a rhombus. Prove that AB2 + BC2 + CD2 + DA2= AC2 + BD2
Sides of triangles are given below. Determine it is a right triangles? In case of a right triangle, write the length of its hypotenuse. 3 cm, 8 cm, 6 cm
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals
A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.

In the given figure, ∆ABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices ?

A boy first goes 5 m due north and then 12 m due east. Find the distance between the initial and the final position of the boy.
The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 60, 61
An isosceles triangle has equal sides each 13 cm and a base 24 cm in length. Find its height
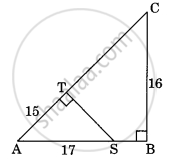
In the given figure, ∠T and ∠B are right angles. If the length of AT, BC and AS (in centimeters) are 15, 16, and 17 respectively, then the length of TC (in centimeters) is ______.
If the hypotenuse of one right triangle is equal to the hypotenuse of another right triangle, then the triangles are congruent.
