Advertisements
Advertisements
प्रश्न
In the given figure, ∆ABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices ?

उत्तर
Let the coordinates of C be (a, b).
Since ∆ABC is an equilateral triangle so, AB = AC = BC = 3 units.
Now,
\[AC = \sqrt{\left( a - 2 \right)^2 + \left( b - 0 \right)^2}\]
\[\text{Squaring on both sides, we have}\]
\[ {AC}^2 = \left( a - 2 \right)^2 + \left( b \right)^2 \]
\[ \Rightarrow {AC}^2 = a^2 + 4 - 4a + b^2 . . . . . \left( 1 \right)\]
Since AB = 3 units, so the coordinates of B will be (5, 0) as the point B is 3 units away from A(2, 0) on the x-axis.
\[\therefore BC = \sqrt{\left( a - 5 \right)^2 + \left( b - 0 \right)^2}\]
\[\text{Squaring on both sides, we have}\]
\[ {BC}^2 = \left( a - 5 \right)^2 + \left( b \right)^2 \]
\[ \Rightarrow {BC}^2 = a^2 + 25 - 10a + b^2 . . . . . \left( 2 \right)\]
From (1) and (2), we have
\[a^2 + 4 - 4a + b^2 = a^2 + 25 - 10a + b^2 \]
\[ \Rightarrow 10a - 4a = 25 - 4\]
\[ \Rightarrow 6a = 21\]
\[ \Rightarrow a = \frac{21}{6} = \frac{7}{2}\]
Substituting `a=7/2` in (1), we have
\[ \Rightarrow 9 = \left( \frac{3}{2} \right)^2 + b^2 \]
\[ \Rightarrow b^2 = 9 - \frac{9}{4} = \frac{27}{4}\]
\[ \Rightarrow b = \pm \frac{3\sqrt{3}}{2}\]
APPEARS IN
संबंधित प्रश्न
In triangle ABC, ∠C=90°. Let BC= a, CA= b, AB= c and let 'p' be the length of the perpendicular from 'C' on AB, prove that:
1. cp = ab
2. `1/p^2=1/a^2+1/b^2`
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2 + BD2 = AB2 + DE2
ABC is a triangle right angled at C. If AB = 25 cm and AC = 7 cm, find BC.
AD is drawn perpendicular to base BC of an equilateral triangle ABC. Given BC = 10 cm, find the length of AD, correct to 1 place of decimal.
If in a ΔPQR, PR2 = PQ2 + QR2, then the right angle of ∆PQR is at the vertex ________
Find the unknown side in the following triangles
Find the length of the support cable required to support the tower with the floor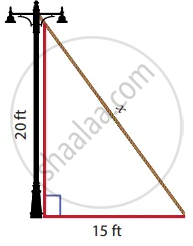
Sides AB and BE of a right triangle, right-angled at B are of lengths 16 cm and 8 cm respectively. The length of the side of largest square FDGB that can be inscribed in the triangle ABE is ______.

If the areas of two circles are the same, they are congruent.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its top reach?
