Advertisements
Advertisements
प्रश्न
M andN are the mid-points of the sides QR and PQ respectively of a PQR, right-angled at Q.
Prove that:
(i) PM2 + RN2 = 5 MN2
(ii) 4 PM2 = 4 PQ2 + QR2
(iii) 4 RN2 = PQ2 + 4 QR2(iv) 4 (PM2 + RN2) = 5 PR2
उत्तर
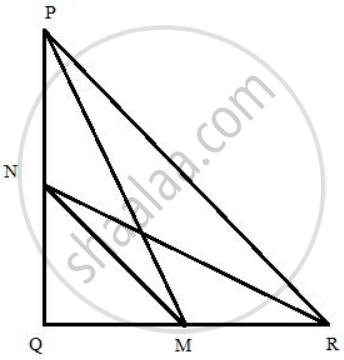
We draw, PM, MN, NR
Pythagoras theorem states that in a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
Since M and N are the mid-points of the sides QR and PQ respectively, therefore, PN = NQ, QM = RM
(i) First, we consider the ΔPQM, and applying Pythagoras theorem we get,
PM2 = PQ2 + MQ2
= ( PN + NQ )2 + MQ2
= PN + NQ2 + 2PN . NQ + MQ2
= MN2+ PN2 + 2PN.NQ ...[From, ΔMNQ, MN2 = NQ2 + MQ2] ......(i)
Now, we consider the ΔRNQ, and applying Pythagoras theorem we get,
RN2 = NQ2 + RQ2
= NQ2 + ( QM + RM )2
= NQ2 + QM2 + RM2 + 2QM .RM
= MN2 + RM2 + 2QM . RM .......(ii)
Adding (i) and (ii) we get,
PM2 + RN2 = MN2 + PN2 + 2PN.NQ + MN2 + RM2 + 2QM. RM
PM2 + RN2 = 2MN2 + PN2 + RM2 + 2PN.NQ + 2QM.RM
PM2 + RN2 = 2MN2 + NQ2 + QM2 + 2(QN2 ) + 2(QM2 )
PM2 + RN2 = 2MN2 + MN2 + 2MN2
PM2 + RN2 = 5MN2
Hence Proved.
(ii) We consider the ΔPQM, and applying Pythagoras theorem we get,
PM2 = PQ2 + MQ2
4PM2 = 4PQ2 + 4MQ2 ...[ Multiply both sides by 4]
4PM2 = 4PQ2 + 4.`(1/2 "QR")^2` ...[ MQ = `1/2` QR ]
4PM2 = 4PQ2 + 4PQ + 4 . `1/4` QR2
4PM2 = 4PQ2 + QR2
Hence Proved.
(iii) We consider the ΔRQN, and applying Pythagoras theorem we get,
RN2 = NQ2 + RQ2
4RN2 = 4NQ2 + 4QR2 ...[ Multiplying both sides by 4]
4RN2 = 4QR2 + 4 .(1/2 PQ)2 ...[ NQ = `1/2` PQ ]
4RN2 = 4QR2 + 4 .`1/4` PQ2
4RN2 = PQ2 + 4QR2
Hence Proved.
(iv) First, we consider the ΔPQM, and applying Pythagoras theorem we get,
PM2 = PQ2 + MQ2
= ( PN + NQ )2 + MQ2
= PN2 + NQ2 + 2PN.NQ + MQ2
= MN2 + PN2 + 2PN.NQ ...[ From, ΔMNQ, = MN2 = NQ2 + MQ2 ] ......(i)
Now, we consider the ΔRNQ, and applying Pythagoras theorem we get,
RN2 + NQ2 + RQ2
= NQ2 + ( QM + RM )2
= NQ2 + QM2 + RM2 + 2QM .RM
= MN2 + RM2 + 2QM . RM .......(ii)
Adding (i) and (ii) we get,
PM2 + RN2 = MN2 + PN2 + 2PN . NQ + MN2 + RM2 + 2QM. RM
PM2 + RN2 = 2MN2 + PN2 + RM2 + 2PN . NQ + 2QM . RM
PM2 + RN2 = 2MN2 + NQ2 + QM2 + 2(QN2 ) + 2(QM2 )
PM2 + RN2 = 2MN2 + MN2 + 2MN2
PM 2 + RN2 = 5MN2
4( PM2 + RN2 ) = 4.5. (NQ2 + MQ2)
4( PM2 + RN2 ) = 4.5. `[ ( 1/2 "PQ" )^2 + ( 1/2 "RQ" )^2 ] ....[ ∵ "NQ" = 1/2 "PQ" , "MQ" = 1/2 "QR" ]`
4 ( PM2 + RN2 ) = 5PR2
Hence Proved.
APPEARS IN
संबंधित प्रश्न
ABC is a triangle right angled at C. If AB = 25 cm and AC = 7 cm, find BC.
Identify, with reason, if the following is a Pythagorean triplet.
(3, 5, 4)
Identify, with reason, if the following is a Pythagorean triplet.
(24, 70, 74)
In figure AB = BC and AD is perpendicular to CD.
Prove that: AC2 = 2BC. DC.
In the following figure, OP, OQ, and OR are drawn perpendiculars to the sides BC, CA and AB respectively of triangle ABC.
Prove that: AR2 + BP2 + CQ2 = AQ2 + CP2 + BR2

If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2) = (AB2 + PQ2)
Find the side of the square whose diagonal is `16sqrt(2)` cm.
In triangle PQR, angle Q = 90°, find: PQ, if PR = 34 cm and QR = 30 cm
The sides of the triangle are given below. Find out which one is the right-angled triangle?
8, 15, 17
A man goes 10 m due east and then 24 m due north. Find the distance from the straight point.
In an equilateral triangle ABC, the side BC is trisected at D. Prove that 9 AD2 = 7 AB2.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
AD is perpendicular to the side BC of an equilateral ΔABC. Prove that 4AD2 = 3AB2.
PQR is an isosceles triangle with PQ = PR = 10 cm and QR = 12 cm. Find the length of the perpendicular from P to QR.
In triangle ABC, line I, is a perpendicular bisector of BC.
If BC = 12 cm, SM = 8 cm, find CS
Two trees 7 m and 4 m high stand upright on a ground. If their bases (roots) are 4 m apart, then the distance between their tops is ______.
Height of a pole is 8 m. Find the length of rope tied with its top from a point on the ground at a distance of 6 m from its bottom.
Points A and B are on the opposite edges of a pond as shown in figure. To find the distance between the two points, the surveyor makes a right-angled triangle as shown. Find the distance AB.

The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. If the ladder is shifted in such a way that its foot is 8 m away from the wall, to what height does its top reach?
