Advertisements
Advertisements
प्रश्न
PQR is an isosceles triangle with PQ = PR = 10 cm and QR = 12 cm. Find the length of the perpendicular from P to QR.
उत्तर
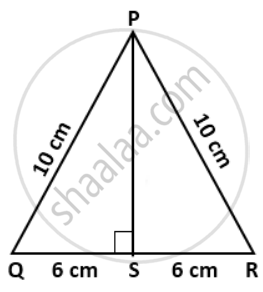
Since, PQR is an isosceles triangle and PS ⊥ QR,
therefore it divides QR into two equal parts.
In ΔPSQ, ∠S = 90°
∴ PQ2 = PS2 + QS2 ....(By Pythagoras Theorem)
⇒ PS2 = PQ2 - QS2
= 102 - 62
= 100 - 36
= 64
⇒ PS = 8cm.
APPEARS IN
संबंधित प्रश्न
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 50 cm, 80 cm, 100 cm
In an equilateral triangle ABC, D is a point on side BC such that BD = `1/3BC` . Prove that 9 AD2 = 7 AB2
In the given figure, ABC is a triangle in which ∠ABC < 90° and AD ⊥ BC. Prove that AC2 = AB2 + BC2 − 2BC.BD.

Which of the following can be the sides of a right triangle?
1.5 cm, 2 cm, 2.5 cm
In the case of right-angled triangles, identify the right angles.
Some question and their alternative answer are given. Select the correct alternative.
If a, b, and c are sides of a triangle and a2 + b2 = c2, name the type of triangle.
In the figure, given below, AD ⊥ BC.
Prove that: c2 = a2 + b2 - 2ax.
In the following figure, OP, OQ, and OR are drawn perpendiculars to the sides BC, CA and AB respectively of triangle ABC.
Prove that: AR2 + BP2 + CQ2 = AQ2 + CP2 + BR2

If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2) = (AB2 + PQ2)
Find the length of diagonal of the square whose side is 8 cm.
Prove that (1 + cot A - cosec A ) (1 + tan A + sec A) = 2
A ladder, 6.5 m long, rests against a vertical wall. If the foot of the ladder is 2.5 m from the foot of the wall, find up to how much height does the ladder reach?
Find the Pythagorean triplet from among the following set of numbers.
3, 4, 5
Find the length of the perpendicular of a triangle whose base is 5cm and the hypotenuse is 13cm. Also, find its area.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
In a right-angled triangle PQR, right-angled at Q, S and T are points on PQ and QR respectively such as PT = SR = 13 cm, QT = 5 cm and PS = TR. Find the length of PQ and PS.
Sides AB and BE of a right triangle, right-angled at B are of lengths 16 cm and 8 cm respectively. The length of the side of largest square FDGB that can be inscribed in the triangle ABE is ______.

Foot of a 10 m long ladder leaning against a vertical wall is 6 m away from the base of the wall. Find the height of the point on the wall where the top of the ladder reaches.
In a quadrilateral ABCD, ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2
[Hint: Produce AB and DC to meet at E.]
Jiya walks 6 km due east and then 8 km due north. How far is she from her starting place?
