Advertisements
Advertisements
प्रश्न
PQR is an isosceles triangle with PQ = PR = 10 cm and QR = 12 cm. Find the length of the perpendicular from P to QR.
उत्तर
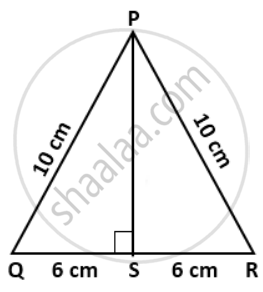
Since, PQR is an isosceles triangle and PS ⊥ QR,
therefore it divides QR into two equal parts.
In ΔPSQ, ∠S = 90°
∴ PQ2 = PS2 + QS2 ....(By Pythagoras Theorem)
⇒ PS2 = PQ2 - QS2
= 102 - 62
= 100 - 36
= 64
⇒ PS = 8cm.
APPEARS IN
संबंधित प्रश्न
If ABC is an equilateral triangle of side a, prove that its altitude = ` \frac { \sqrt { 3 } }{ 2 } a`
In a ∆ABC, AD ⊥ BC and AD2 = BC × CD. Prove ∆ABC is a right triangle
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 50 cm, 80 cm, 100 cm
In the following figure, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that

(i) OA2 + OB2 + OC2 − OD2 − OE2 − OF2 = AF2 + BD2 + CE2
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2
A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
In the given figure, M is the midpoint of QR. ∠PRQ = 90°. Prove that, PQ2 = 4PM2 – 3PR2.

In right angle ΔABC, if ∠B = 90°, AB = 6, BC = 8, then find AC.
A ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
If the sides of the triangle are in the ratio 1: `sqrt2`: 1, show that is a right-angled triangle.
O is any point inside a rectangle ABCD.
Prove that: OB2 + OD2 = OC2 + OA2.
In triangle ABC, ∠B = 90o and D is the mid-point of BC.
Prove that: AC2 = AD2 + 3CD2.
The top of a ladder of length 15 m reaches a window 9 m above the ground. What is the distance between the base of the wall and that of the ladder?
Find the Pythagorean triplet from among the following set of numbers.
2, 6, 7
Calculate the area of a right-angled triangle whose hypotenuse is 65cm and one side is 16cm.
A point OI in the interior of a rectangle ABCD is joined with each of the vertices A, B, C and D. Prove that OB2 + OD2 = OC2 + OA2
If ‘l‘ and ‘m’ are the legs and ‘n’ is the hypotenuse of a right angled triangle then, l2 = ________
In a right-angled triangle ABC, if angle B = 90°, BC = 3 cm and AC = 5 cm, then the length of side AB is ______.
Two rectangles are congruent, if they have same ______ and ______.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. Find the length of the ladder.
