Advertisements
Advertisements
प्रश्न
A ladder 13 m long rests against a vertical wall. If the foot of the ladder is 5 m from the foot of the wall, find the distance of the other end of the ladder from the ground.
उत्तर
The pictorial representation of the given problem is given below,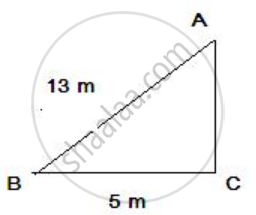
Pythagoras theorem states that in a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
Here, AB is the hypotenuse.
Therefore applying the Pythagoras theorem we get,
AB2 = BC2 + CA2
132 = 52 + CA2
CA2 = 132 - 52
CA2 = 144
CA = 12 m
Therefore, the distance of the other end of the ladder from the ground is 12m.
APPEARS IN
संबंधित प्रश्न
The points A(4, 7), B(p, 3) and C(7, 3) are the vertices of a right traingle ,right-angled at B. Find the values of p.
If ABC is an equilateral triangle of side a, prove that its altitude = ` \frac { \sqrt { 3 } }{ 2 } a`
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 50 cm, 80 cm, 100 cm
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
In the given figure, ABC is a triangle in which ∠ABC> 90° and AD ⊥ CB produced. Prove that AC2 = AB2 + BC2 + 2BC.BD.

Pranali and Prasad started walking to the East and to the North respectively, from the same point and at the same speed. After 2 hours distance between them was \[15\sqrt{2}\]
km. Find their speed per hour.
In ∆ABC, seg AD ⊥ seg BC, DB = 3CD.
Prove that: 2AB2 = 2AC2 + BC2

A man goes 40 m due north and then 50 m due west. Find his distance from the starting point.
Find the length of diagonal of the square whose side is 8 cm.
Prove that `(sin θ + cosec θ)^2 + (cos θ + sec θ)^2 = 7 + tan^2 θ + cot^2 θ`.
In the given figure, angle ACP = ∠BDP = 90°, AC = 12 m, BD = 9 m and PA= PB = 15 m. Find:
(i) CP
(ii) PD
(iii) CD

Show that the triangle ABC is a right-angled triangle; if: AB = 9 cm, BC = 40 cm and AC = 41 cm
In the figure below, find the value of 'x'.

The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 12, 15
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = AE2 + CD2 + BF2
Find the distance between the helicopter and the ship
In the figure, find AR
The hypotenuse (in cm) of a right angled triangle is 6 cm more than twice the length of the shortest side. If the length of third side is 6 cm less than thrice the length of shortest side, then find the dimensions of the triangle.
The foot of a ladder is 6 m away from its wall and its top reaches a window 8 m above the ground. Find the length of the ladder.
