Advertisements
Advertisements
प्रश्न
A man goes 40 m due north and then 50 m due west. Find his distance from the starting point.
उत्तर
Here, we need to measure the distance AB as shown in the figure below,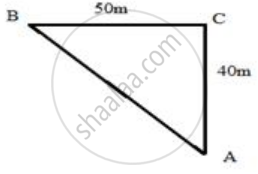
Pythagoras theorem states that in a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
Therefore, in this case
AB2 = BC2 + CA2
AB2 = 502 + 402
AB2 = 2500 + 1600
AB2 = 4100
AB = 64.03
Therefore the required distance is 64.03 m.
APPEARS IN
संबंधित प्रश्न
Two towers of heights 10 m and 30 m stand on a plane ground. If the distance between their feet is 15 m, find the distance between their tops
In figure, ∠B of ∆ABC is an acute angle and AD ⊥ BC, prove that AC2 = AB2 + BC2 – 2BC × BD
P and Q are the mid-points of the sides CA and CB respectively of a ∆ABC, right angled at C. Prove that:
`(i) 4AQ^2 = 4AC^2 + BC^2`
`(ii) 4BP^2 = 4BC^2 + AC^2`
`(iii) (4AQ^2 + BP^2 ) = 5AB^2`
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that AE2 + BD2 = AB2 + DE2
In an equilateral triangle ABC, D is a point on side BC such that BD = `1/3BC` . Prove that 9 AD2 = 7 AB2
Walls of two buildings on either side of a street are parallel to each other. A ladder 5.8 m long is placed on the street such that its top just reaches the window of a building at the height of 4 m. On turning the ladder over to the other side of the street, its top touches the window of the other building at a height 4.2 m. Find the width of the street.
In the given figure, point T is in the interior of rectangle PQRS, Prove that, TS2 + TQ2 = TP2 + TR2 (As shown in the figure, draw seg AB || side SR and A-T-B)

In an isosceles triangle, length of the congruent sides is 13 cm and its base is 10 cm. Find the distance between the vertex opposite the base and the centroid.
Two poles of heights 6 m and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m;
find the distance between their tips.
In triangle ABC, AB = AC = x, BC = 10 cm and the area of the triangle is 60 cm2.
Find x.
Triangle PQR is right-angled at vertex R. Calculate the length of PR, if: PQ = 34 cm and QR = 33.6 cm.
The sides of a certain triangle is given below. Find, which of them is right-triangle
16 cm, 20 cm, and 12 cm
In the figure below, find the value of 'x'.
PQR is an isosceles triangle with PQ = PR = 10 cm and QR = 12 cm. Find the length of the perpendicular from P to QR.
Find the unknown side in the following triangles
In the figure, find AR
From the given figure, in ∆ABQ, if AQ = 8 cm, then AB =?

Foot of a 10 m long ladder leaning against a vertical wall is 6 m away from the base of the wall. Find the height of the point on the wall where the top of the ladder reaches.
In a quadrilateral ABCD, ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2
[Hint: Produce AB and DC to meet at E.]
If two legs of a right triangle are equal to two legs of another right triangle, then the right triangles are congruent.
