Advertisements
Advertisements
प्रश्न
Foot of a 10 m long ladder leaning against a vertical wall is 6 m away from the base of the wall. Find the height of the point on the wall where the top of the ladder reaches.
उत्तर
Let AB be a vertical wall and AC = 10 m is a ladder.
The top of the ladder reaches to A and distance of ladder from the base of the wall BC is 6 m.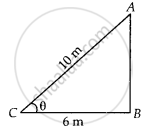
In right angled ΔABC,
AC2 = AB2 + BC2 ...[By pythagoras theorem]
⇒ (10)2 = AB2 + (6)2
⇒ 100 = AB2 + 36
⇒ AB2 = 100 – 36 = 64
∴ AB = `sqrt(64)` = 8 cm
Hence, the height of the point on the wall where the top of the ladder reaches is 8 cm.
APPEARS IN
संबंधित प्रश्न
In triangle ABC, ∠C=90°. Let BC= a, CA= b, AB= c and let 'p' be the length of the perpendicular from 'C' on AB, prove that:
1. cp = ab
2. `1/p^2=1/a^2+1/b^2`
Identify, with reason, if the following is a Pythagorean triplet.
(11, 60, 61)
Find the value of (sin2 33 + sin2 57°)
Find the length of the hypotenuse of a triangle whose other two sides are 24cm and 7cm.
A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
There are two paths that one can choose to go from Sarah’s house to James's house. One way is to take C street, and the other way requires to take B street and then A street. How much shorter is the direct path along C street?

From the given figure, in ∆ABQ, if AQ = 8 cm, then AB =?

From given figure, In ∆ABC, If AC = 12 cm. then AB =?

Activity: From given figure, In ∆ABC, ∠ABC = 90°, ∠ACB = 30°
∴ ∠BAC = `square`
∴ ∆ABC is 30° – 60° – 90° triangle
∴ In ∆ABC by property of 30° – 60° – 90° triangle.
∴ AB = `1/2` AC and `square` = `sqrt(3)/2` AC
∴ `square` = `1/2 xx 12` and BC = `sqrt(3)/2 xx 12`
∴ `square` = 6 and BC = `6sqrt(3)`
In figure, PQR is a right triangle right angled at Q and QS ⊥ PR. If PQ = 6 cm and PS = 4 cm, find QS, RS and QR.
In a triangle, sum of squares of two sides is equal to the square of the third side.
