Advertisements
Advertisements
Question
Foot of a 10 m long ladder leaning against a vertical wall is 6 m away from the base of the wall. Find the height of the point on the wall where the top of the ladder reaches.
Solution
Let AB be a vertical wall and AC = 10 m is a ladder.
The top of the ladder reaches to A and distance of ladder from the base of the wall BC is 6 m.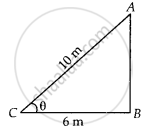
In right angled ΔABC,
AC2 = AB2 + BC2 ...[By pythagoras theorem]
⇒ (10)2 = AB2 + (6)2
⇒ 100 = AB2 + 36
⇒ AB2 = 100 – 36 = 64
∴ AB = `sqrt(64)` = 8 cm
Hence, the height of the point on the wall where the top of the ladder reaches is 8 cm.
APPEARS IN
RELATED QUESTIONS
ABC is a right triangle right-angled at C. Let BC = a, CA = b, AB = c and let p be the length of perpendicular from C on AB, prove that
(i) cp = ab
`(ii) 1/p^2=1/a^2+1/b^2`
ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals
In right angle ΔABC, if ∠B = 90°, AB = 6, BC = 8, then find AC.
AD is drawn perpendicular to base BC of an equilateral triangle ABC. Given BC = 10 cm, find the length of AD, correct to 1 place of decimal.
In the figure, given below, AD ⊥ BC.
Prove that: c2 = a2 + b2 - 2ax.
From the given figure, find the length of hypotenuse AC and the perimeter of ∆ABC.
From a point O in the interior of aΔABC, perpendicular OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: AF2 + BD2 + CE2 = AE2 + CD2 + BF2
AD is perpendicular to the side BC of an equilateral ΔABC. Prove that 4AD2 = 3AB2.
Two angles are said to be ______, if they have equal measures.
