Advertisements
Advertisements
Question
A 15 metres high tower casts a shadow 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 metres long. Find the height of the telephone pole.
Solution
Let BC = 15 m be the tower and its shadow AB is 24 m.
At that time ∠CAB = θ.
Again, let EF = h be a telephone pole and its shadow DE = 16 m.
At the same time ∠EDF = θ.
Here, ΔABC and ΔDEF both are right-angled triangles.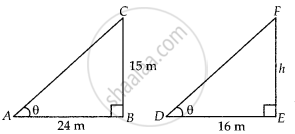
In ΔABC and ΔDEF,
∠CAB = ∠EDF = θ
∠B = ∠E ...[Each 90°]
∴ ΔABC ∼ ΔDEF ...[By AAA similarity criterion]
Then, `("AB")/("DE") = ("BC")/("EF")`
⇒ `24/16 = 15/h`
∴ h = `(15 xx 16)/24` = 10
Hence, the height of the telephone pole is 10 m.
APPEARS IN
RELATED QUESTIONS
State which pair of triangles in the given figure are similar. Write the similarity criterion used by you for answering the question, and also write the pairs of similar triangles in the symbolic form:
A vertical pole of a length 6 m casts a shadow 4m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.
If AD and PM are medians of triangles ABC and PQR, respectively where ΔABC ~ ΔPQR, prove that `("AB")/("PQ") = ("AD")/("PM")`.
In the following figure, XY || BC. Find the length of XY.
In a right angled triangle with sides a and b and hypotenuse c, the altitude drawn on the hypotenuse is x. Prove that ab = cx.
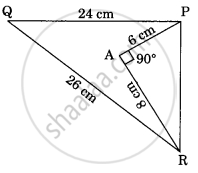
In the given figure, PQ = 24 cm, QR = 26 cm ∠PAR = 90°, PA = 6 cm, and AR = 8 cm, the degree measure of ∠QPR is ______.
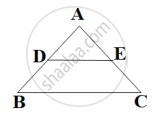
In the figure, if DE∥BC, AD = 3cm, BD = 4cm and BC= 14 cm, then DE equals ______.
In a ∆PQR, PR2 – PQ2 = QR2 and M is a point on side PR such that QM ⊥ PR. Prove that QM2 = PM × MR.
Which of the following is NOT a similarity criterion of traingles?
In ΔABC, DE || AB. If AB = a, DE = x, BE = b and EC = c. Then x expressed in terms of a, b and c is ______.