Advertisements
Advertisements
प्रश्न
A 15 metres high tower casts a shadow 24 metres long at a certain time and at the same time, a telephone pole casts a shadow 16 metres long. Find the height of the telephone pole.
उत्तर
Let BC = 15 m be the tower and its shadow AB is 24 m.
At that time ∠CAB = θ.
Again, let EF = h be a telephone pole and its shadow DE = 16 m.
At the same time ∠EDF = θ.
Here, ΔABC and ΔDEF both are right-angled triangles.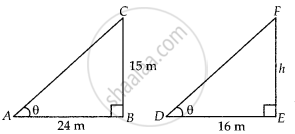
In ΔABC and ΔDEF,
∠CAB = ∠EDF = θ
∠B = ∠E ...[Each 90°]
∴ ΔABC ∼ ΔDEF ...[By AAA similarity criterion]
Then, `("AB")/("DE") = ("BC")/("EF")`
⇒ `24/16 = 15/h`
∴ h = `(15 xx 16)/24` = 10
Hence, the height of the telephone pole is 10 m.
APPEARS IN
संबंधित प्रश्न
S and T are point on sides PR and QR of ΔPQR such that ∠P = ∠RTS. Show that ΔRPQ ∼ ΔRTS.
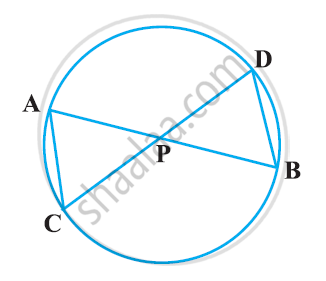
In the given figure, two chords AB and CD intersect each other at the point P. prove that:
(i) ΔAPC ∼ ΔDPB
(ii) AP.BP = CP.DP
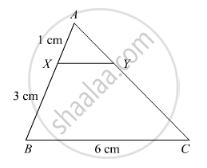
In the following figure, XY || BC. Find the length of XY.
A ladder 10m long reaches the window of a house 8m above the ground. Find the distance of the foot of the ladder from the base of the wall.
D is a point on side QR of ΔPQR such that PD ⊥ QR. Will it be correct to say that ΔPQD ~ ΔRPD? Why?
In figure, if ∠A = ∠C, AB = 6 cm, BP = 15 cm, AP = 12 cm and CP = 4 cm, then find the lengths of PD and CD.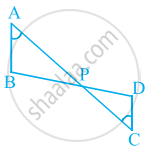
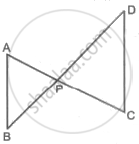
In the above figure, seg AC and seg BD intersect each other in point P. If `("AP")/("CP") = ("BP")/("DP")`, then complete the following activity to prove ΔABP ∼ ΔCDP.
Activity: In ΔABP and ΔCDP
`("AP")/("CP") = ("BP")/("DP")` ......`square`
∴ ∠APB ≅ `square` ......Vertically opposite angles
∴ `square` ∼ ΔCDP ....... `square` test of similarity.
In ΔABC, seg XY || side AC. If 2AX = 3BX and XY = 9, then find the value of AC.

In the given figure, ΔPQR is a right-angled triangle with ∠PQR = 90°. QS is perpendicular to PR. Prove that pq = rx.

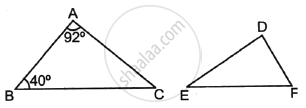
If ΔABC ∼ ΔDEF such that ∠A = 92° and ∠B = 40°, then ∠F = ?