Advertisements
Advertisements
प्रश्न
Foot of a 10 m long ladder leaning against a vertical wall is 6 m away from the base of the wall. Find the height of the point on the wall where the top of the ladder reaches.
उत्तर
Let AB be a vertical wall and AC = 10 m is a ladder.
The top of the ladder reaches to A and distance of ladder from the base of the wall BC is 6 m.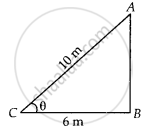
In right angled ΔABC,
AC2 = AB2 + BC2 ...[By pythagoras theorem]
⇒ (10)2 = AB2 + (6)2
⇒ 100 = AB2 + 36
⇒ AB2 = 100 – 36 = 64
∴ AB = `sqrt(64)` = 8 cm
Hence, the height of the point on the wall where the top of the ladder reaches is 8 cm.
APPEARS IN
संबंधित प्रश्न
In Fig., ∆ABC is an obtuse triangle, obtuse angled at B. If AD ⊥ CB, prove that AC2 = AB2 + BC2 + 2BC × BD
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AB2 = BC × BD

In the given figure, ∠DFE = 90°, FG ⊥ ED, If GD = 8, FG = 12, find (1) EG (2) FD and (3) EF

Find the length diagonal of a rectangle whose length is 35 cm and breadth is 12 cm.
In a trapezium ABCD, seg AB || seg DC seg BD ⊥ seg AD, seg AC ⊥ seg BC, If AD = 15, BC = 15 and AB = 25. Find A(▢ABCD)

In triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC.

A man goes 10 m due east and then 24 m due north. Find the distance from the straight point.
An isosceles triangle has equal sides each 13 cm and a base 24 cm in length. Find its height
The longest side of a right angled triangle is called its ______.
If the areas of two circles are the same, they are congruent.
