Advertisements
Advertisements
प्रश्न
In triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC.

उत्तर
We have Pythagoras theorem which states that in a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
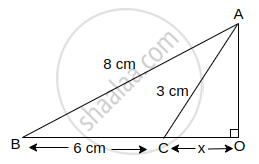
In Δ AOC,
AC2 = AO2 + CO2
(3)2 = AO2 + x2
9 = AO2 + x2
9 - x2 = AO2 ...(i)
In Δ AOB,
AB2 = AO2 + BO2
(8)2 = AO2 + (6 + x)2
64 = AO2 + (6 + x)2
64 - (6 + x)2 = AO2 ...(ii)
From equation (i) and (ii)
9 - x2 = 64 - (6 + x)2
9 - x2 = 64 - (36 + x2 + 12x) ...[(a + b)2 = a2 + 2ab + b2]
9 - x2 = 64 - 36 - x2 - 12x
9 = 28 - 12x
12x = 28 - 9
x = `19/12`
x = `1 7/12`
APPEARS IN
संबंधित प्रश्न
ABCD is a rectangle whose three vertices are B (4, 0), C(4, 3) and D(0,3). The length of one of its diagonals is
(A) 5
(B) 4
(C) 3
(D) 25
ABC is a right-angled triangle, right-angled at A. A circle is inscribed in it. The lengths of the two sides containing the right angle are 5 cm and 12 cm. Find the radius of the circle
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM2 = QM . MR
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AB2 = BC × BD

In the given figure, M is the midpoint of QR. ∠PRQ = 90°. Prove that, PQ2 = 4PM2 – 3PR2.

Find the length of the hypotenuse of a right angled triangle if remaining sides are 9 cm and 12 cm.
Two poles of heights 6 m and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m;
find the distance between their tips.
In triangle ABC, AB = AC and BD is perpendicular to AC.
Prove that: BD2 - CD2 = 2CD × AD
If the angles of a triangle are 30°, 60°, and 90°, then shown that the side opposite to 30° is half of the hypotenuse, and the side opposite to 60° is `sqrt(3)/2` times of the hypotenuse.
Find the value of (sin2 33 + sin2 57°)
Triangle XYZ is right-angled at vertex Z. Calculate the length of YZ, if XY = 13 cm and XZ = 12 cm.
A ladder, 6.5 m long, rests against a vertical wall. If the foot of the ladder is 2.5 m from the foot of the wall, find up to how much height does the ladder reach?
Find the Pythagorean triplet from among the following set of numbers.
4, 5, 6
Find the length of the hypotenuse of a triangle whose other two sides are 24cm and 7cm.
Calculate the area of a right-angled triangle whose hypotenuse is 65cm and one side is 16cm.
A man goes 10 m due east and then 24 m due north. Find the distance from the straight point.
In ∆PQR, PD ⊥ QR such that D lies on QR. If PQ = a, PR = b, QD = c and DR = d, prove that (a + b)(a – b) = (c + d)(c – d).
In a quadrilateral ABCD, ∠A + ∠D = 90°. Prove that AC2 + BD2 = AD2 + BC2
[Hint: Produce AB and DC to meet at E.]
In an equilateral triangle PQR, prove that PS2 = 3(QS)2.

Two trees 7 m and 4 m high stand upright on a ground. If their bases (roots) are 4 m apart, then the distance between their tops is ______.
