Advertisements
Advertisements
प्रश्न
In triangle ABC, given below, AB = 8 cm, BC = 6 cm and AC = 3 cm. Calculate the length of OC.
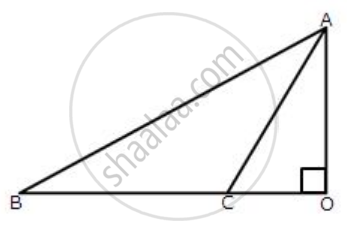
उत्तर
We have Pythagoras theorem which states that in a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
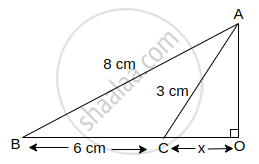
In Δ AOC,
AC2 = AO2 + CO2
(3)2 = AO2 + x2
9 = AO2 + x2
9 - x2 = AO2 ...(i)
In Δ AOB,
AB2 = AO2 + BO2
(8)2 = AO2 + (6 + x)2
64 = AO2 + (6 + x)2
64 - (6 + x)2 = AO2 ...(ii)
From equation (i) and (ii)
9 - x2 = 64 - (6 + x)2
9 - x2 = 64 - (36 + x2 + 12x) ...[(a + b)2 = a2 + 2ab + b2]
9 - x2 = 64 - 36 - x2 - 12x
9 = 28 - 12x
12x = 28 - 9
x = `19/12`
x = `1 7/12`
APPEARS IN
संबंधित प्रश्न
In triangle ABC, ∠C=90°. Let BC= a, CA= b, AB= c and let 'p' be the length of the perpendicular from 'C' on AB, prove that:
1. cp = ab
2. `1/p^2=1/a^2+1/b^2`
ABCD is a rhombus. Prove that AB2 + BC2 + CD2 + DA2= AC2 + BD2
The perpendicular AD on the base BC of a ∆ABC intersects BC at D so that DB = 3 CD. Prove that `2"AB"^2 = 2"AC"^2 + "BC"^2`
In the given figure, ABC is a triangle in which ∠ABC < 90° and AD ⊥ BC. Prove that AC2 = AB2 + BC2 − 2BC.BD.

Identify, with reason, if the following is a Pythagorean triplet.
(10, 24, 27)
In the given figure, point T is in the interior of rectangle PQRS, Prove that, TS2 + TQ2 = TP2 + TR2 (As shown in the figure, draw seg AB || side SR and A-T-B)

In triangle ABC, angle A = 90o, CA = AB and D is the point on AB produced.
Prove that DC2 - BD2 = 2AB.AD.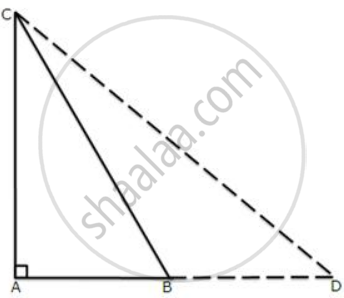
In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
Prove that: 2AC2 - AB2 = BC2 + CD2 + DA2
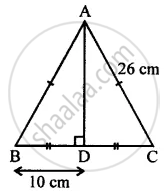
In the given figure, angle ADB = 90°, AC = AB = 26 cm and BD = DC. If the length of AD = 24 cm; find the length of BC.
The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 60, 61
A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
In ΔABC, AD is perpendicular to BC. Prove that: AB2 + CD2 = AC2 + BD2
In the given figure, PQ = `"RS"/(3)` = 8cm, 3ST = 4QT = 48cm.
SHow that ∠RTP = 90°.
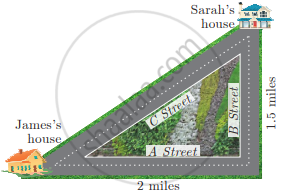
There are two paths that one can choose to go from Sarah’s house to James's house. One way is to take C street, and the other way requires to take B street and then A street. How much shorter is the direct path along C street?
Find the unknown side in the following triangles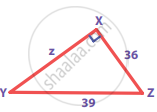
In triangle ABC, line I, is a perpendicular bisector of BC.
If BC = 12 cm, SM = 8 cm, find CS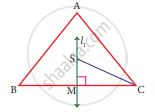
If S is a point on side PQ of a ΔPQR such that PS = QS = RS, then ______.
Prove that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle.
Two angles are said to be ______, if they have equal measures.
Two squares having same perimeter are congruent.
