Advertisements
Advertisements
प्रश्न
In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
Prove that: 2AC2 - AB2 = BC2 + CD2 + DA2
उत्तर
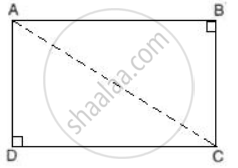
In quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
So, ΔABC and ΔADC are right-angled triangles.
In ΔABC, using Pythagoras theorem,
AC2 = AB2 + BC2
⇒ AB2 = AC2 - BC2 ....(i)
In ΔADC, using Pythagoras theorem,
AC2 = AD2 + DC2 ....(ii)
LHS = 2AC2 - AB2
= 2AC2 - ( AC2 - BC2 ) .....[ From(i) ]
= 2AC2 - AC2 + BC2
= AC2 + BC2
= AD2 + DC2 + BC2 ....[ From(ii) ]
= RHS
APPEARS IN
संबंधित प्रश्न
If ABC is an equilateral triangle of side a, prove that its altitude = ` \frac { \sqrt { 3 } }{ 2 } a`
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 50 cm, 80 cm, 100 cm
In Figure ABD is a triangle right angled at A and AC ⊥ BD. Show that AC2 = BC × DC

Which of the following can be the sides of a right triangle?
2 cm, 2 cm, 5 cm
In the case of right-angled triangles, identify the right angles.
The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.
In triangle ABC, angle A = 90o, CA = AB and D is the point on AB produced.
Prove that DC2 - BD2 = 2AB.AD.
In Fig. 3, ∠ACB = 90° and CD ⊥ AB, prove that CD2 = BD x AD.

In ∆ ABC, AD ⊥ BC.
Prove that AC2 = AB2 +BC2 − 2BC x BD
Use the information given in the figure to find the length AD.

In an equilateral triangle ABC, the side BC is trisected at D. Prove that 9 AD2 = 7 AB2.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2AD2 + `(1)/(2)"BC"^2`
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that: 9BP2 = 9BC2 + 4AC2
In a right-angled triangle PQR, right-angled at Q, S and T are points on PQ and QR respectively such as PT = SR = 13 cm, QT = 5 cm and PS = TR. Find the length of PQ and PS.
To get from point A to point B you must avoid walking through a pond. You must walk 34 m south and 41 m east. To the nearest meter, how many meters would be saved if it were possible to make a way through the pond?
In a right angled triangle, if length of hypotenuse is 25 cm and height is 7 cm, then what is the length of its base?
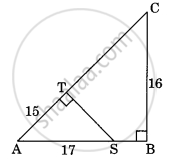
In the given figure, ∠T and ∠B are right angles. If the length of AT, BC and AS (in centimeters) are 15, 16, and 17 respectively, then the length of TC (in centimeters) is ______.
In ΔABC, if DE || BC, AD = x, DB = x – 2, AE = x + 2 and EC = x – 1, then value of x is ______.
Height of a pole is 8 m. Find the length of rope tied with its top from a point on the ground at a distance of 6 m from its bottom.
