Advertisements
Advertisements
प्रश्न
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that: 9BP2 = 9BC2 + 4AC2
उत्तर
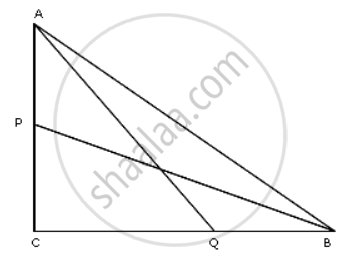
P divides AC in the ratio 2 : 1
So C.P. = `(2)/(3) "AC"` .......(i)
Q divides BC in the ratio 2 : 1
QC = `(2)/(3)"BC"` ......(ii)
Applying Pythagoras theorem in right triangle BCP, we have
BP2 = BC2 + CP2
⇒ BP2 = `"BC"^2 + (4)/(9)"AC"^2` ...(Using (i))
⇒ 9BP2 = 9BC2 + 4AC2.
APPEARS IN
संबंधित प्रश्न
In triangle ABC, ∠C=90°. Let BC= a, CA= b, AB= c and let 'p' be the length of the perpendicular from 'C' on AB, prove that:
1. cp = ab
2. `1/p^2=1/a^2+1/b^2`
The points A(4, 7), B(p, 3) and C(7, 3) are the vertices of a right traingle ,right-angled at B. Find the values of p.
An aeroplane leaves an airport and flies due north at a speed of 1,000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1,200 km per hour. How far apart will be the two planes after `1 1/2` hours?
ABC is a triangle right angled at C. If AB = 25 cm and AC = 7 cm, find BC.
Identify, with reason, if the following is a Pythagorean triplet.
(10, 24, 27)
Some question and their alternative answer are given. Select the correct alternative.
If a, b, and c are sides of a triangle and a2 + b2 = c2, name the type of triangle.
Pranali and Prasad started walking to the East and to the North respectively, from the same point and at the same speed. After 2 hours distance between them was \[15\sqrt{2}\]
km. Find their speed per hour.

In ΔMNP, ∠MNP = 90˚, seg NQ ⊥ seg MP, MQ = 9, QP = 4, find NQ.
In ΔABC, Find the sides of the triangle, if:
- AB = ( x - 3 ) cm, BC = ( x + 4 ) cm and AC = ( x + 6 ) cm
- AB = x cm, BC = ( 4x + 4 ) cm and AC = ( 4x + 5) cm
In the given figure, AB//CD, AB = 7 cm, BD = 25 cm and CD = 17 cm;
find the length of side BC.
AD is drawn perpendicular to base BC of an equilateral triangle ABC. Given BC = 10 cm, find the length of AD, correct to 1 place of decimal.
In a quadrilateral ABCD, ∠B = 90° and ∠D = 90°.
Prove that: 2AC2 - AB2 = BC2 + CD2 + DA2
In triangle ABC, ∠B = 90o and D is the mid-point of BC.
Prove that: AC2 = AD2 + 3CD2.
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2 ) = (AB2 + PQ2)
In the figure below, find the value of 'x'.

In the right-angled ∆PQR, ∠ P = 90°. If l(PQ) = 24 cm and l(PR) = 10 cm, find the length of seg QR.
AD is perpendicular to the side BC of an equilateral ΔABC. Prove that 4AD2 = 3AB2.
In a square PQRS of side 5 cm, A, B, C and D are points on sides PQ, QR, RS and SP respectively such as PA = PD = RB = RC = 2 cm. Prove that ABCD is a rectangle. Also, find the area and perimeter of the rectangle.
Find the unknown side in the following triangles
Jiya walks 6 km due east and then 8 km due north. How far is she from her starting place?
