Advertisements
Advertisements
प्रश्न
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2 ) = (AB2 + PQ2)
उत्तर
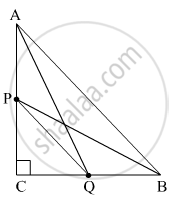
Using the Pythagoras theorem in ΔABC, ΔACQ, ΔBPC, ΔPCQ, we get
AB2 = AC2 + BC2 ......(1)
AQ2 = AC2 + CQ2 ......(2)
BP2 = PC2 + BC2 .......(3)
PQ2 = PC2 + CQ2 .......(4)
Adding the equations (2) and (3) we get
AQ2 + BP2 = AC2 + CQ2 + PC2 + BC2
= (AC2 + BC2) + (CQ + PC2)
= AB2 + PQ2
As
L.H.S. = AQ2 + BP2
= AB2 + PQ2
= R.H.S
Hence Proved
संबंधित प्रश्न
ABC is a right triangle right-angled at C. Let BC = a, CA = b, AB = c and let p be the length of perpendicular from C on AB, prove that
(i) cp = ab
`(ii) 1/p^2=1/a^2+1/b^2`
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM2 = QM . MR
ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2
Identify, with reason, if the following is a Pythagorean triplet.
(3, 5, 4)
In figure AB = BC and AD is perpendicular to CD.
Prove that: AC2 = 2BC. DC.
In triangle PQR, angle Q = 90°, find: PR, if PQ = 8 cm and QR = 6 cm
From the given figure, find the length of hypotenuse AC and the perimeter of ∆ABC.
Rithika buys an LED TV which has a 25 inches screen. If its height is 7 inches, how wide is the screen? Her TV cabinet is 20 inches wide. Will the TV fit into the cabinet? Give reason
Foot of a 10 m long ladder leaning against a vertical wall is 6 m away from the base of the wall. Find the height of the point on the wall where the top of the ladder reaches.
A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
