Advertisements
Advertisements
प्रश्न
From the given figure, find the length of hypotenuse AC and the perimeter of ∆ABC.
उत्तर
Given here is a right-angled triangle. So, we can apply Pythagoras theorem.
AB2 + BC2 = AC2
⇒ 202 + 212 = AC2
⇒ AC2 = 400 + 441 = 841
⇒ AC = 29
Thus, the length of hypotenuse is 29 units.
Perimeter of ∆ABC = AB + BC + CA = 20 + 21 + 29 = 70 units.
APPEARS IN
संबंधित प्रश्न
In the following figure, O is a point in the interior of a triangle ABC, OD ⊥ BC, OE ⊥ AC and OF ⊥ AB. Show that

(i) OA2 + OB2 + OC2 − OD2 − OE2 − OF2 = AF2 + BD2 + CE2
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2
PQR is a triangle right angled at P. If PQ = 10 cm and PR = 24 cm, find QR.
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2) = (AB2 + PQ2)
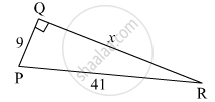
In the figure below, find the value of 'x'.
The sides of the triangle are given below. Find out which one is the right-angled triangle?
1.5, 1.6, 1.7
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 + AC2 = 2(AD2 + CD2)
Find the distance between the helicopter and the ship
Find the length of the support cable required to support the tower with the floor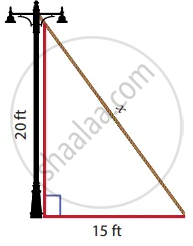
If ΔABC ~ ΔPQR, `("ar" triangle "ABC")/("ar" triangle "PQR") = 9/4` and AB = 18 cm, then the length of PQ is ______.
If the hypotenuse of one right triangle is equal to the hypotenuse of another right triangle, then the triangles are congruent.
