Advertisements
Advertisements
प्रश्न
PQR is a triangle right angled at P. If PQ = 10 cm and PR = 24 cm, find QR.
उत्तर
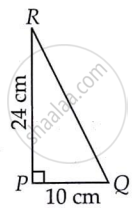
By applying Pythagoras theorem in ΔPQR,
(PQ)2 + (PR)2 = (RQ)2
(10)2 + (24)2 = RQ2
100 + 576 = (QR)2
676 = (QR)2
QR = 26 cm
APPEARS IN
संबंधित प्रश्न
ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals
In ΔABC, Find the sides of the triangle, if:
- AB = ( x - 3 ) cm, BC = ( x + 4 ) cm and AC = ( x + 6 ) cm
- AB = x cm, BC = ( 4x + 4 ) cm and AC = ( 4x + 5) cm
O is any point inside a rectangle ABCD.
Prove that: OB2 + OD2 = OC2 + OA2.
The top of a ladder of length 15 m reaches a window 9 m above the ground. What is the distance between the base of the wall and that of the ladder?
Find the Pythagorean triplet from among the following set of numbers.
2, 6, 7
The sides of the triangle are given below. Find out which one is the right-angled triangle?
11, 12, 15
A ladder 25m long reaches a window of a building 20m above the ground. Determine the distance of the foot of the ladder from the building.
The hypotenuse of a right angled triangle of sides 12 cm and 16 cm is __________
Two squares are congruent, if they have same ______.
