Advertisements
Advertisements
प्रश्न
O is any point inside a rectangle ABCD.
Prove that: OB2 + OD2 = OC2 + OA2.
उत्तर
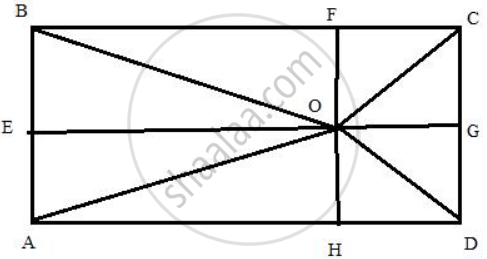
Draw rectangle ABCD with arbitrary point O within it, and then draw lines OA, OB, OC, OD. Then draw lines from point O perpendicular to the sides: OE, OF, OG, OH.
Pythagoras theorem states that in a right-angled triangle, the square on the hypotenuse is equal to the sum of the squares on the remaining two sides.
Using Pythagorean theorem we have from the above diagram:
OA2 = AH2 + OH2 = AH2 + AE2
OC2 = CG2 + OG2 = EB2 + HD2
OB2 = EO2 + BE2 = AH2 + BE2
OD2 = HD2 + OH2 = HD2 + AE2
Adding these equalities we get:
OA2 + OC2 = AH2 + HD2 + AE2 + EB2
OB2 + OD2 = AH2 + HD2 + AE2 + EB2
From which we prove that for any point within the rectangle there is the relation
OA2 + OC2 = OB2 + OD2
Hence Proved.
APPEARS IN
संबंधित प्रश्न
In triangle ABC, ∠C=90°. Let BC= a, CA= b, AB= c and let 'p' be the length of the perpendicular from 'C' on AB, prove that:
1. cp = ab
2. `1/p^2=1/a^2+1/b^2`
The diagonal of a rectangular field is 16 metres more than the shorter side. If the longer side is 14 metres more than the shorter side, then find the lengths of the sides of the field.
In Fig., ∆ABC is an obtuse triangle, obtuse angled at B. If AD ⊥ CB, prove that AC2 = AB2 + BC2 + 2BC × BD
ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2
ABC is an isosceles triangle with AC = BC. If AB2 = 2AC2, prove that ABC is a right triangle.
Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.
Identify, with reason, if the following is a Pythagorean triplet.
(3, 5, 4)
Find the side and perimeter of a square whose diagonal is 10 cm.
Pranali and Prasad started walking to the East and to the North respectively, from the same point and at the same speed. After 2 hours distance between them was \[15\sqrt{2}\]
km. Find their speed per hour.
In ΔABC, Find the sides of the triangle, if:
- AB = ( x - 3 ) cm, BC = ( x + 4 ) cm and AC = ( x + 6 ) cm
- AB = x cm, BC = ( 4x + 4 ) cm and AC = ( 4x + 5) cm
Prove that (1 + cot A - cosec A ) (1 + tan A + sec A) = 2
The sides of a certain triangle is given below. Find, which of them is right-triangle
6 m, 9 m, and 13 m
In the given figure, angle BAC = 90°, AC = 400 m, and AB = 300 m. Find the length of BC.

Two poles of height 9m and 14m stand on a plane ground. If the distance between their 12m, find the distance between their tops.
In a triangle ABC, AC > AB, D is the midpoint BC, and AE ⊥ BC. Prove that: AB2 = AD2 - BC x CE + `(1)/(4)"BC"^2`
In a triangle ABC right angled at C, P and Q are points of sides CA and CB respectively, which divide these sides the ratio 2 : 1.
Prove that : 9(AQ2 + BP2) = 13AB2
A 5 m long ladder is placed leaning towards a vertical wall such that it reaches the wall at a point 4 m high. If the foot of the ladder is moved 1.6 m towards the wall, then find the distance by which the top of the ladder would slide upwards on the wall.
If S is a point on side PQ of a ΔPQR such that PS = QS = RS, then ______.
Height of a pole is 8 m. Find the length of rope tied with its top from a point on the ground at a distance of 6 m from its bottom.
Two poles of 10 m and 15 m stand upright on a plane ground. If the distance between the tops is 13 m, find the distance between their feet.
