Advertisements
Advertisements
प्रश्न
Find the side and perimeter of a square whose diagonal is 10 cm.
उत्तर
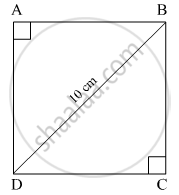
Let ABCD be the given square.
AC = 10 cm
Let the side of the square be x cm.
∴ AB = BC = x cm
In Δ ABC,
∠ABC = 90° ...(Angle of a square)
∴ by Pythagoras theorem,
AC2 = AB2 + BC2
∴ 102 = x2 + x2
∴ 100 = 2x2
∴ x2 = `100/2`
∴ x2 = 50
∴ x = `5sqrt2`
∴ AB = `5sqrt2` cm
∴ side of a square is `5sqrt2` cm.
Perimeter of a square = 4 × side
= 4 × `5sqrt2`
= `20sqrt2` cm
∴ Side of a square is `5sqrt2` cm and its perimeter is `20sqrt2` cm.
APPEARS IN
संबंधित प्रश्न
Sides of triangle are given below. Determine it is a right triangle or not? In case of a right triangle, write the length of its hypotenuse. 7 cm, 24 cm, 25 cm
In Figure, ABD is a triangle right angled at A and AC ⊥ BD. Show that AD2 = BD × CD

ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2
A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.
In the given figure, M is the midpoint of QR. ∠PRQ = 90°. Prove that, PQ2 = 4PM2 – 3PR2.

In the given figure, point T is in the interior of rectangle PQRS, Prove that, TS2 + TQ2 = TP2 + TR2 (As shown in the figure, draw seg AB || side SR and A-T-B)


In ΔMNP, ∠MNP = 90˚, seg NQ ⊥ seg MP, MQ = 9, QP = 4, find NQ.
In ΔABC, Find the sides of the triangle, if:
- AB = ( x - 3 ) cm, BC = ( x + 4 ) cm and AC = ( x + 6 ) cm
- AB = x cm, BC = ( 4x + 4 ) cm and AC = ( 4x + 5) cm
In the figure: ∠PSQ = 90o, PQ = 10 cm, QS = 6 cm and RQ = 9 cm. Calculate the length of PR.
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2) = (AB2 + PQ2)
The sides of a certain triangle is given below. Find, which of them is right-triangle
16 cm, 20 cm, and 12 cm
The sides of a certain triangle is given below. Find, which of them is right-triangle
6 m, 9 m, and 13 m
From the given figure, find the length of hypotenuse AC and the perimeter of ∆ABC.
A man goes 10 m due east and then 24 m due north. Find the distance from the straight point.
In an equilateral triangle ABC, the side BC is trisected at D. Prove that 9 AD2 = 7 AB2.
Find the unknown side in the following triangles
In triangle ABC, line I, is a perpendicular bisector of BC.
If BC = 12 cm, SM = 8 cm, find CS
In a right angled triangle, if length of hypotenuse is 25 cm and height is 7 cm, then what is the length of its base?
In an isosceles triangle PQR, the length of equal sides PQ and PR is 13 cm and base QR is 10 cm. Find the length of perpendicular bisector drawn from vertex P to side QR.
The longest side of a right angled triangle is called its ______.
