Advertisements
Advertisements
प्रश्न
If P and Q are the points on side CA and CB respectively of ΔABC, right angled at C, prove that (AQ2 + BP2) = (AB2 + PQ2)
उत्तर
Using the Pythagoras theorem in ΔABC,
ΔACQ, ΔBPC, ΔPCQ, we get
AB2 = AC2 + BC2 ..(1)
AQ2 = AC2 + CQ2 ...(2)
BP2 = PC2 + BC2 ..(3)
PQ2 = PC2 + CO2 ...(4)
Adding the equations (2) and (3) we get
AQ2 + BP2 = AC2 + CQ2 + PC2 + BC2
=(AC2 + BC2) + (CQ2 + PC2)
= AB2 + PQ2
As L.H.S = AQ2 + BP2
= AB2 + PQ2 = R.H.S
APPEARS IN
संबंधित प्रश्न
In triangle ABC, ∠C=90°. Let BC= a, CA= b, AB= c and let 'p' be the length of the perpendicular from 'C' on AB, prove that:
1. cp = ab
2. `1/p^2=1/a^2+1/b^2`
In the figure: ∠PSQ = 90o, PQ = 10 cm, QS = 6 cm and RQ = 9 cm. Calculate the length of PR.
Find the length of diagonal of the square whose side is 8 cm.
Find the Pythagorean triplet from among the following set of numbers.
4, 7, 8
A ladder 25m long reaches a window of a building 20m above the ground. Determine the distance of the foot of the ladder from the building.
A ladder 15m long reaches a window which is 9m above the ground on one side of a street. Keeping its foot at the same point, the ladder is turned to other side of the street to reach a window 12m high. Find the width of the street.
In a right-angled triangle ABC,ABC = 90°, AC = 10 cm, BC = 6 cm and BC produced to D such CD = 9 cm. Find the length of AD.
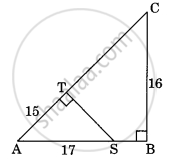
In the given figure, ∠T and ∠B are right angles. If the length of AT, BC and AS (in centimeters) are 15, 16, and 17 respectively, then the length of TC (in centimeters) is ______.
If the areas of two circles are the same, they are congruent.
Points A and B are on the opposite edges of a pond as shown in figure. To find the distance between the two points, the surveyor makes a right-angled triangle as shown. Find the distance AB.

