Advertisements
Advertisements
प्रश्न
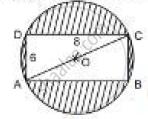
Find the area of the shaded region in the figure If ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle. (Take π= 3.14)
उत्तर
Here, diagonal AC also represents the diameter of the circle.
Using Pythagoras theorem:
AC = `sqrt(AB^2 + BC^2)`
AC = `sqrt(8^2 + 6^2)`
AC = `sqrt(64 + 36)`
AC = `sqrt100`
AC = 10
RAdius of the circle, OC = `"AC"/2 = 5 "cm"`
Area of the shaded region = Area of the circle - Area of rectangle
= `pi"r"^2 - "AB"xx"BC"`
= `pi ("OC")^2 - "AB"xx"BC"`
= 3.14 x 52 - 8 x 6
= 78.5 - 48
= 30.5
Therefore, the area of shaded region is 30.5 cm2 .
APPEARS IN
संबंधित प्रश्न
In Fig. 1, PA and PB are tangents to the circle with centre O such that ∠APB = 50°. Write the measure of ∠OAB.

Fill in the blanks:
The centre of a circle lies in ____________ of the circle.
O is the center of a circle of radius 8cm. The tangent at a point A on the circle cuts a line through O at B such that AB = 15 cm. Find OB
In the given figure, O is the centre of the circle and ∠DAB = 50° . Calculate the values of xand y.

If AB, BC and CD are equal chords of a circle with O as centre and AD diameter, than ∠AOB =
Construct a triangle PQR in which, PQ = QR = RP = 5.7 cm. Draw the incircle of the triangle and measure its radius.
Given: A circle inscribed in a right angled ΔABC. If ∠ACB = 90° and the radius of the circle is r.
To prove: 2r = a + b – c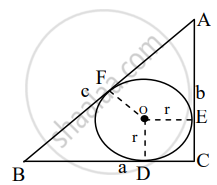
The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA = 110°, find ∠CBA see figure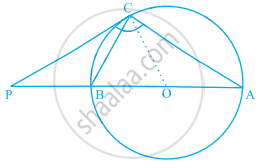
If AB = 12 cm, BC = 16 cm and AB is perpendicular to BC, then the radius of the circle passing through the points A, B and C is ______.
Draw any circle and mark
- it's centre
- a radius
- a diameter
- a sector
- a segment
- a point in its interior
- a point in its exterior
- an arc
