Advertisements
Advertisements
प्रश्न
If AB, BC and CD are equal chords of a circle with O as centre and AD diameter, than ∠AOB =
विकल्प
60°
90°
120°
none of these
उत्तर
60°
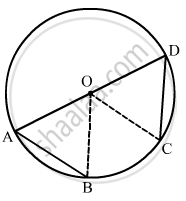
As we know that equal chords make equal angle at the centre.
Therefore,
\[\angle AOB = \angle BOC = \angle COD\]
\[\angle AOB + \angle BOC + \angle COD = 180° \left[ \text{ Linear pair } \right]\]
\[ \Rightarrow 3\angle AOB = 180°\]
\[ \Rightarrow \angle AOB = 60° \]
APPEARS IN
संबंधित प्रश्न
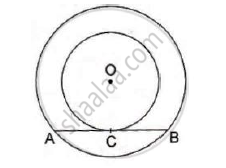
In the given figure, the chord AB of the larger of the two concentric circles, with center O, touches the smaller circle at C. Prove that AC = CB.
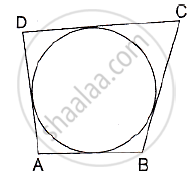
In the adjoining figure, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB=6cm, BC=9cm and CD=8 cm. Find the length of side AD.
In the given figure, PO \[\perp\] QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OTare right bisector of each other.

Draw a line AB = 8.4 cm. Now draw a circle with AB as diameter. Mark a point C on the circumference of the circle. Measure angle ACB.
In a circle with centre P, chord AB is parallel to a tangent and intersects the radius drawn from the point of contact to its midpoint. If AB = `16sqrt(3)`, then find the radius of the circle
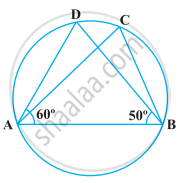
In the following figure, if ∠DAB = 60º, ∠ABD = 50º, then ∠ACB is equal to ______.
In the following figure, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.

A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
Assertion (A): If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason (R): Circumference = 2π × radius of a circle.
