Advertisements
Advertisements
प्रश्न
Assertion (A): If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason (R): Circumference = 2π × radius of a circle.
विकल्प
Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of the Assertion (A).
Both Assertion (A) and Reason (R) are true, but Reason (R) is not the correct explanation of the Assertion (A).
Assertion (A) is true, but Reason (R) is false.
Assertion (A) is false, but Reason (R) is true.
उत्तर
Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of the Assertion (A).
Explanation:
Circumference = 176 cm
Circumference = 2πr ...(where 'r' is the radius of circle)
⇒ 176 = `2xx22/7xx"r"`
⇒ 176 × 7 = 2 × 22 × r
⇒ 1232 = 44r
⇒ `1232/44` = r
⇒ r = 28
∴ The radius of the circle = 28 cm
APPEARS IN
संबंधित प्रश्न
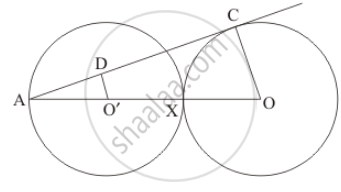
Equal circles with centres O and O' touch each other at X. OO' produced to meet a circle with centre O', at A. AC is a tangent to the circle whose centre is O. O'D is perpendicular to AC. Find the value of\[\frac{DO'}{CO}\]
Radius of a circle with centre O is 4 cm. If l(OP) = 4.2 cm, say where point P will lie.
Draw a circle of radius of 4.2 cm. Mark its center as O. Takes a point A on the circumference of the circle. Join AO and extend it till it meets point B on the circumference of the circle,
(i) Measure the length of AB.
(ii) Assign a special name to AB.
In the table below, write the names of the points in the interior and exterior of the circle and those on the circle.
| Diagram | Points in the interior of the circle |
Points in the exterior of the circle |
Points on the circle |
 |
A chord is at a distance of 15 cm from the centre of the circle of radius 25 cm. The length of the chord is
The radius of a circle of diameter 24 cm is _______
In the figure, segment PQ is the diameter of the circle with center O. The tangent to the tangent circle drawn from point C on it, intersects the tangents drawn from points P and Q at points A and B respectively, prove that ∠AOB = 90°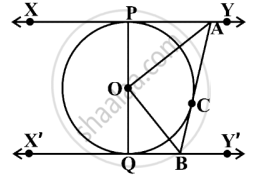
In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
[Hint: Draw a line through Q and perpendicular to QP.]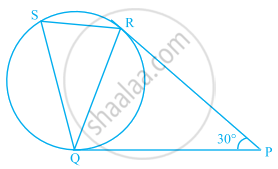
The circumcentre of the triangle ABC is O. Prove that ∠OBC + ∠BAC = 90º.
From the figure, identify the centre of the circle.